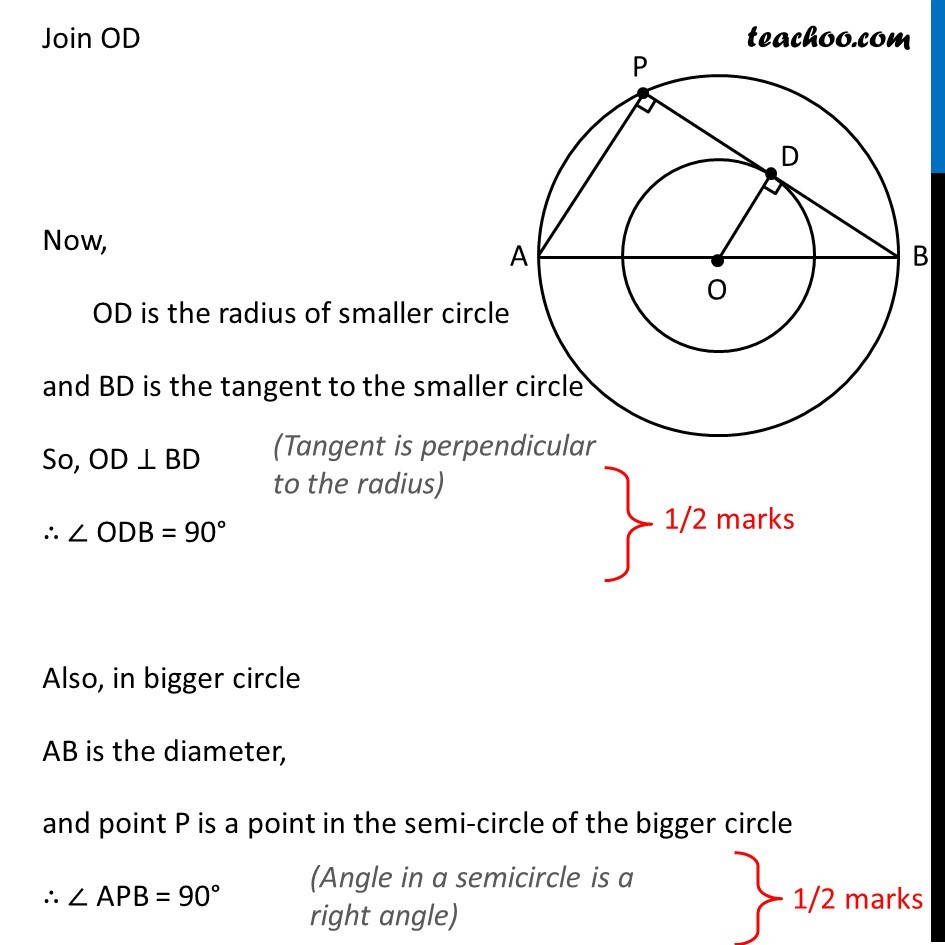
Check sibling questions

CBSE Class 10 Sample Paper for 2019 Boards

CBSE Class 10 Sample Paper for 2018 Boards →
Class 10
Solutions of Sample Papers for Class 10 Boards

Question 18 - CBSE Class 10 Sample Paper for 2019 Boards - Solutions of Sample Papers for Class 10 Boards

Last updated at March 23, 2023 by

Question 18

The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of AP

The radii of two concentric circles are 13 cm and 8 cm. AB is diameter

Question 18 - CBSE Class 10 Sample Paper for 2019 Boards - Part 2
Question 18 - CBSE Class 10 Sample Paper for 2019 Boards - Part 3

This video is only available for Teachoo black users

Subscribe Now

Get live Maths 1-on-1 Classs - Class 6 to 12

Book 30 minute class for ₹ 499 ₹ 299

Transcript

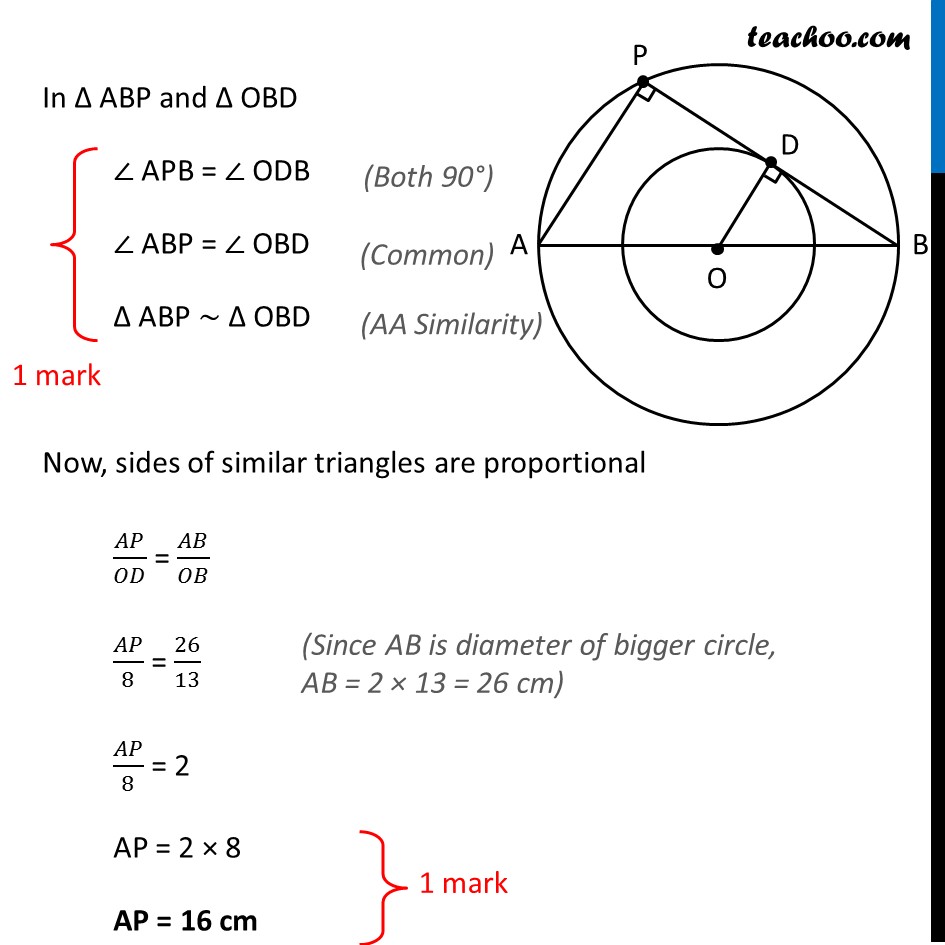
Question 18 The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of AP Let’s first draw the figure We need to find length of AP Join OD Now, OD is the radius of smaller circle and BD is the tangent to the smaller circle So, OD ⊥ BD (Tangent is perpendicular to the radius) ∴ ∠ ODB = 90° Also, in bigger circle AB is the diameter, and point P is a point in the semi-circle of the bigger circle ∴ ∠ APB = 90° (Tangent is perpendicular to the radius) In Δ ABP and Δ OBD ∠ APB = ∠ ODB Both 90°) ∠ ABP = ∠ OBD (Common) Δ ABP ~ Δ OBD (AA Similarity) Now, sides of similar triangles are proportional 𝐴𝑃/𝑂𝐷 = 𝐴𝐵/𝑂𝐵 𝐴𝑃/8 = 26/13 (Since AB is diameter of bigger circle, AB = 2 × 13 = 26 cm) 𝐴𝑃/8 = 2 AP = 2 × 8 AP = 16 cm We need to find length of AP

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.