




Ex 5.4
Last updated at Dec. 16, 2024 by Teachoo






Transcript
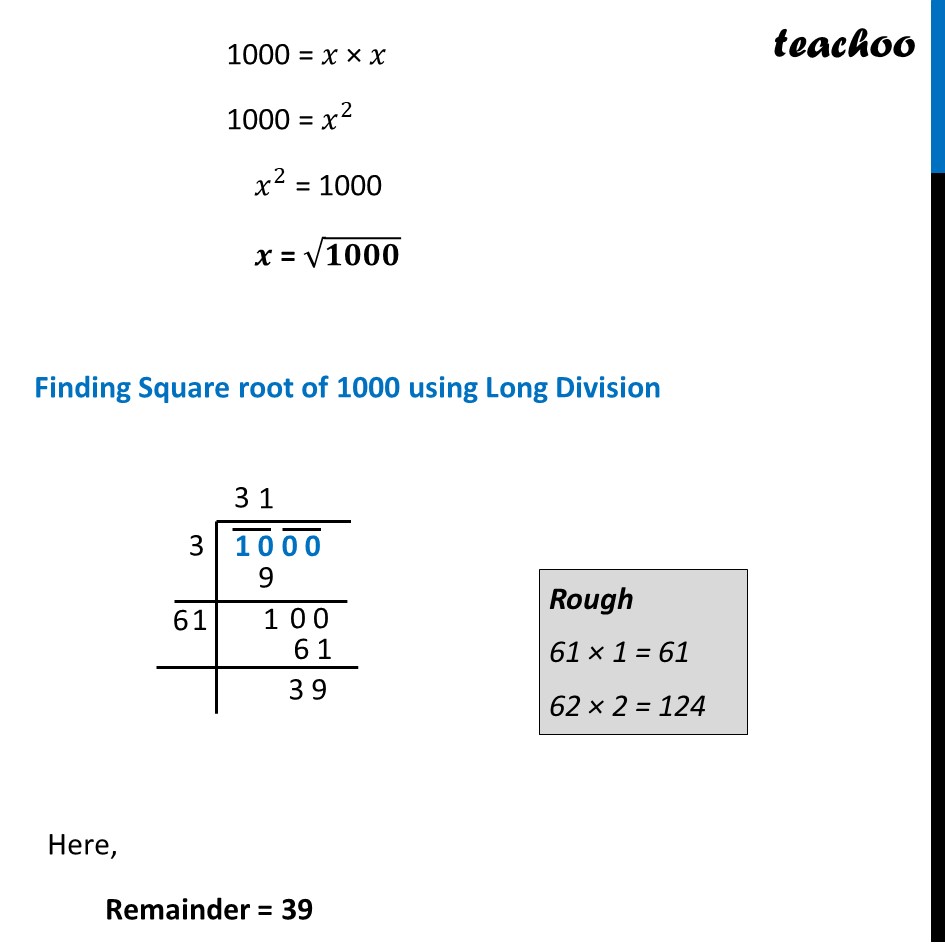
Ex 5.4, 8 (Introduction) A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this. Let Total number of rows = 3 And Total number of columns = 3 Total Plants = Number of plants in 1st row + Number of plants in 2nd row + Number of plants in 3rd row = 3 + 3 + 3 = 3 × 3 = 9 So we can say that Total Plants = Number of rows × Number of columns Ex 5.4, 8 A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this.Given Total Plants = 1000 And number of rows is equal to the number of columns Let Number of rows = 𝑥 ∴ Number of columns = 𝑥 Now, Total Plants = Number of Rows × Number of columns 1000 = 𝑥 × 𝑥 1000 = 𝑥^2 𝑥^2 = 1000 𝒙 = √𝟏𝟎𝟎𝟎 Finding Square root of 1000 using Long Division Here, Remainder = 39 Given that, He wants to plant these in such a way that the number of rows and the number of columns remain same, we need to find the minimum number of plants he needs more for this. We need to find the least number that must be added to 1000 so as to get a perfect square Now, Thus, we add 322 – 1000 to the number ∴ Number to added = 322 − 1000 = 1024 – 1000 = 24 ∴ The Gardner needs 24 more plants.