


Ex 10.1
Last updated at Dec. 16, 2024 by Teachoo







Transcript
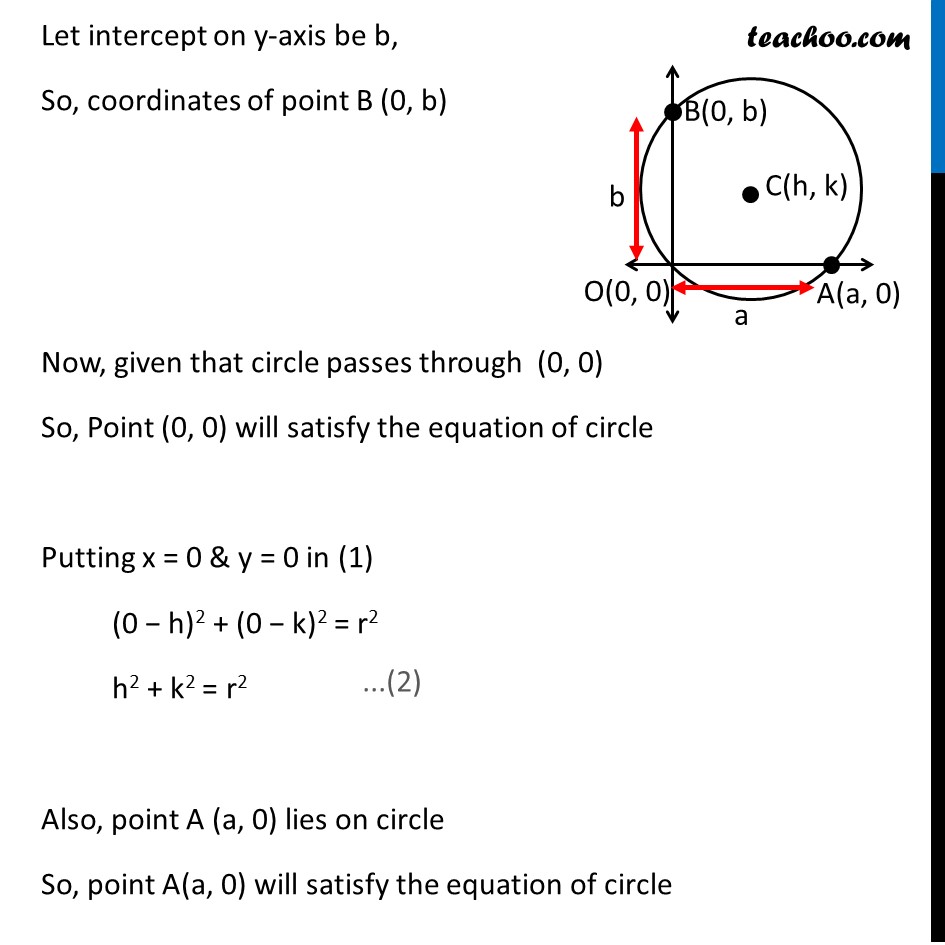
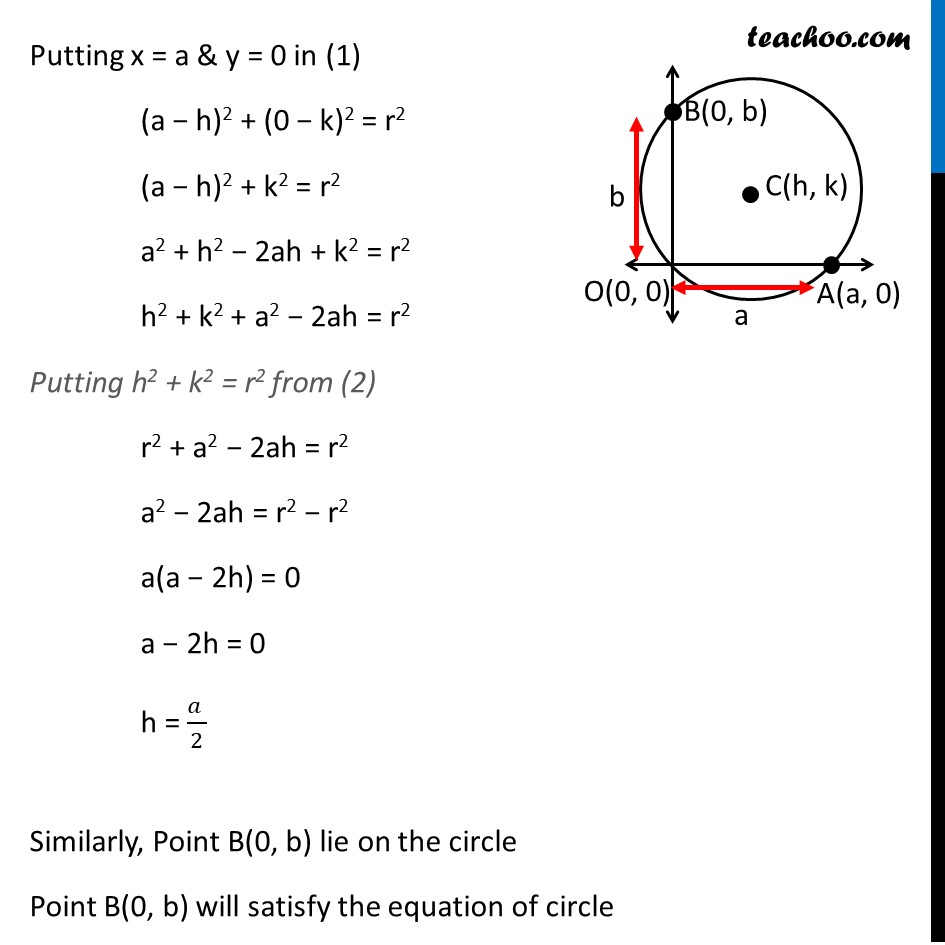
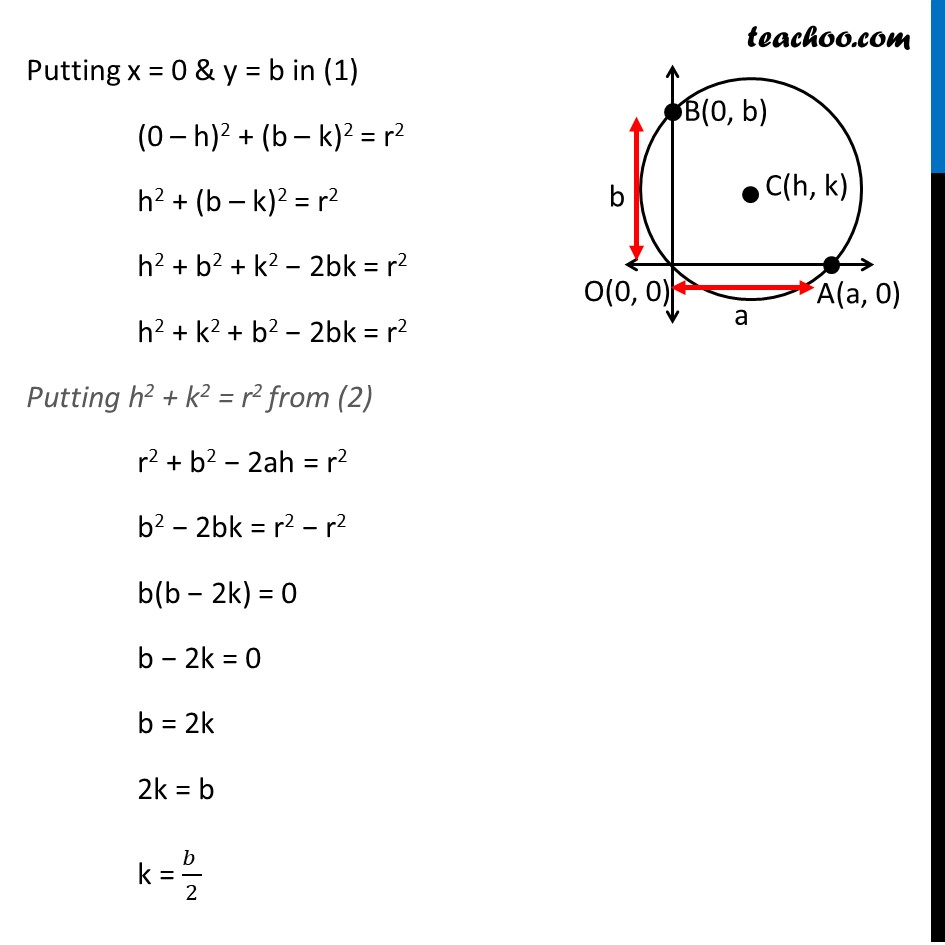
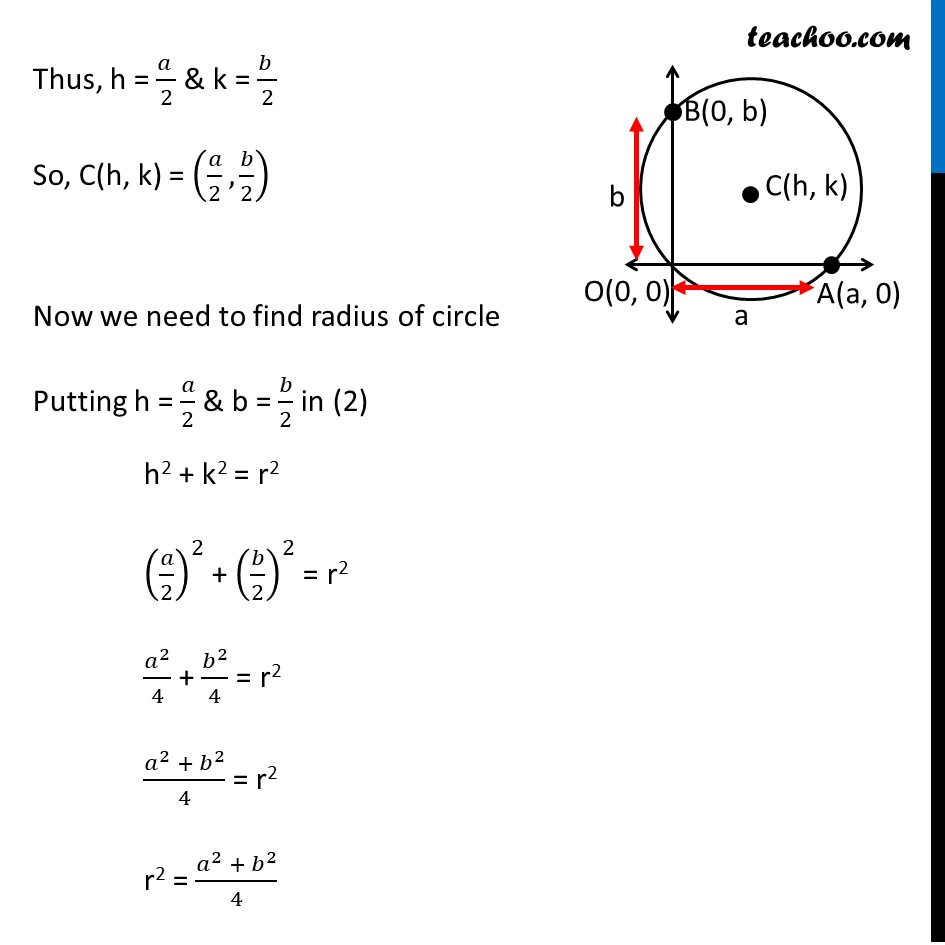
Ex 10.1, 13 Find the equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes. Let the equation of circle be (x – h)2 + (y – k)2 = r2 where (h, k) is the centre & r is the radius of a circle Also given that circle making intercepts a & b on the coordinate axes Let intercept on x-axis be a, So, coordinates of point A (a, 0) Let intercept on y-axis be b, So, coordinates of point B (0, b) Now, given that circle passes through (0, 0) So, Point (0, 0) will satisfy the equation of circle Putting x = 0 & y = 0 in (1) (0 − h)2 + (0 − k)2 = r2 h2 + k2 = r2 Also, point A (a, 0) lies on circle So, point A(a, 0) will satisfy the equation of circle Putting x = a & y = 0 in (1) (a − h)2 + (0 − k)2 = r2 (a − h)2 + k2 = r2 a2 + h2 − 2ah + k2 = r2 h2 + k2 + a2 − 2ah = r2 Putting h2 + k2 = r2 from (2) r2 + a2 − 2ah = r2 a2 − 2ah = r2 − r2 a(a − 2h) = 0 a − 2h = 0 h = (𝑎 )/2 Similarly, Point B(0, b) lie on the circle Point B(0, b) will satisfy the equation of circle Putting x = 0 & y = b in (1) (0 – h)2 + (b – k)2 = r2 h2 + (b – k)2 = r2 h2 + b2 + k2 − 2bk = r2 h2 + k2 + b2 − 2bk = r2 Putting h2 + k2 = r2 from (2) r2 + b2 − 2ah = r2 b2 − 2bk = r2 − r2 b(b − 2k) = 0 b − 2k = 0 b = 2k 2k = b k = (𝑏 )/2 Thus, h = (𝑎 )/2 & k = (𝑏 )/2 So, C(h, k) = (𝑎/2, 𝑏/2) Now we need to find radius of circle Putting h = 𝑎/2 & b = 𝑏/2 in (2) h2 + k2 = r2 (𝑎/2)^2 + (𝑏/2)^2 = r2 𝑎^2/4 + 𝑏^2/4 = r2 〖𝑎^2 + 𝑏〗^2/4 = r2 r2 = 〖𝑎^2 + 𝑏〗^2/4 Putting value of (h, k) & r2 in (1) (x – h)2 + (y – k)2 = r2 (𝑥− 𝑎/2)^2 + (𝑦−𝑏/2)^2 = 〖𝑎^2 + 𝑏〗^2/4 (x)2 + (𝑎/2)^2 − 2(x) (𝑎/2) + y2 +(𝑏/2)^2 − 2(y) (𝑏/2) = 〖𝑎^2 + 𝑏〗^2/4 x2 + 𝑎^2/4 − ax + y2 + 𝑏^2/4 − by = 〖𝑎^2 + 𝑏〗^2/4 x2 + y2 − ax − by + 𝑎^2/4 + 𝑏^2/4 = 〖𝑎^2 + 𝑏〗^2/4 x2 + y2 − ax − by + 〖𝑎^2 + 𝑏〗^2/4 = 〖𝑎^2 + 𝑏〗^2/4 x2 + y2 − ax − by = (𝑎2 + 𝑏2)/4 − 〖𝑎^2 + 𝑏〗^2/4 x2 + y2 − ax − by = 0 Which is required equation of circle