Example 3 - Chapter 13 Class 10 Surface Areas and Volumes (Important Question)

Transcript

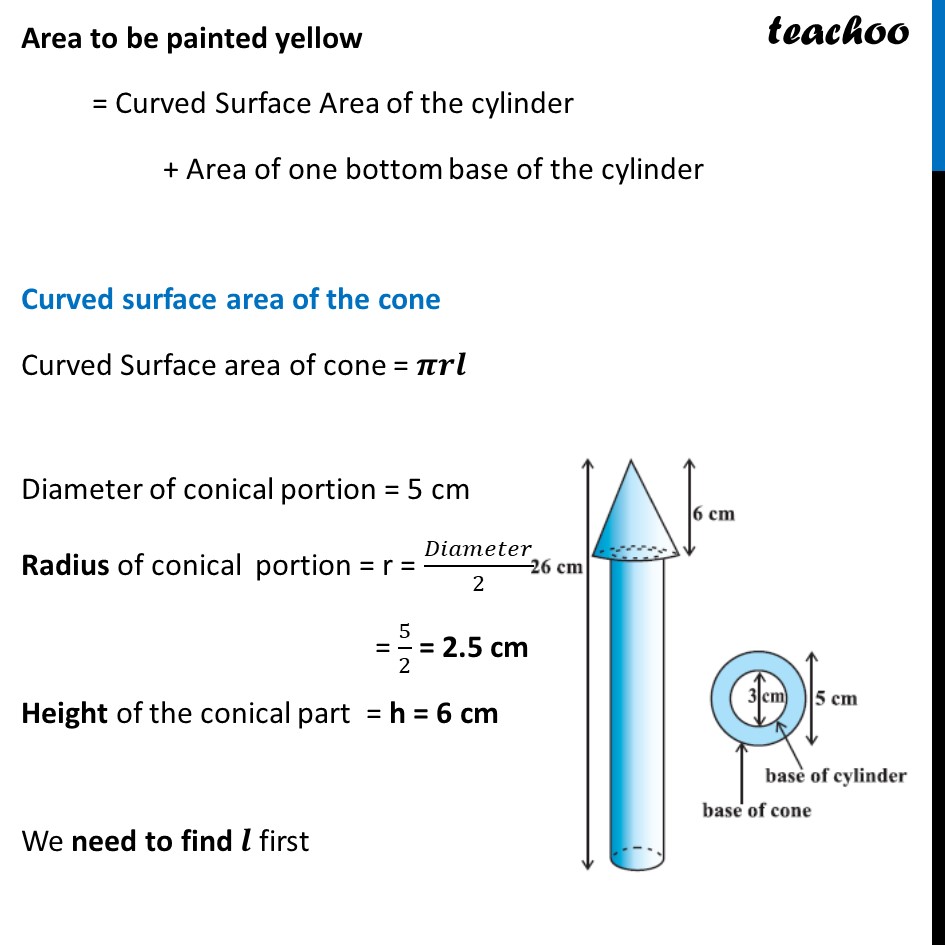
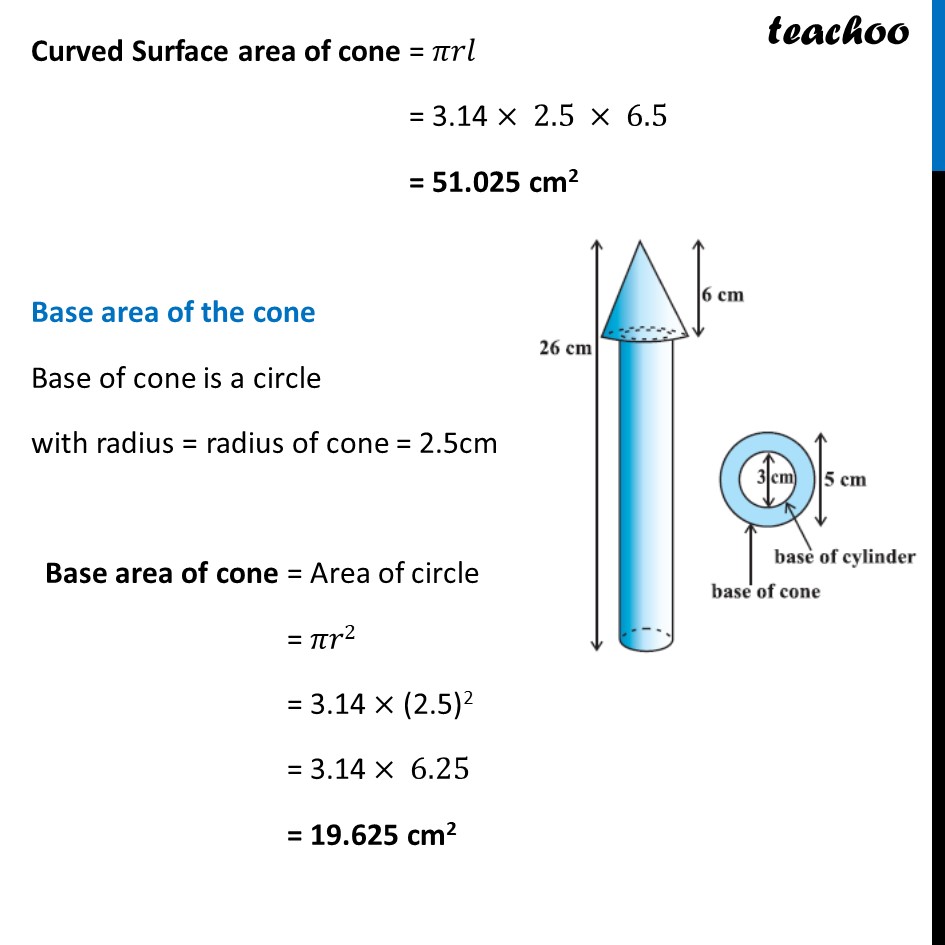
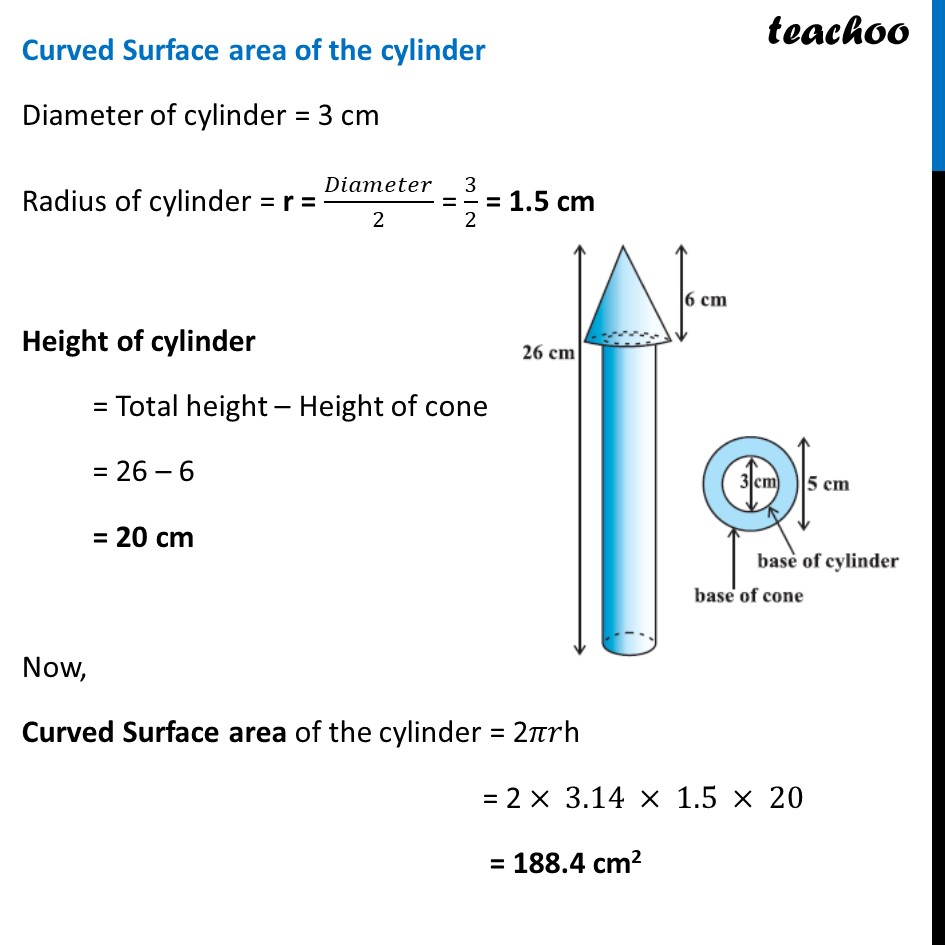
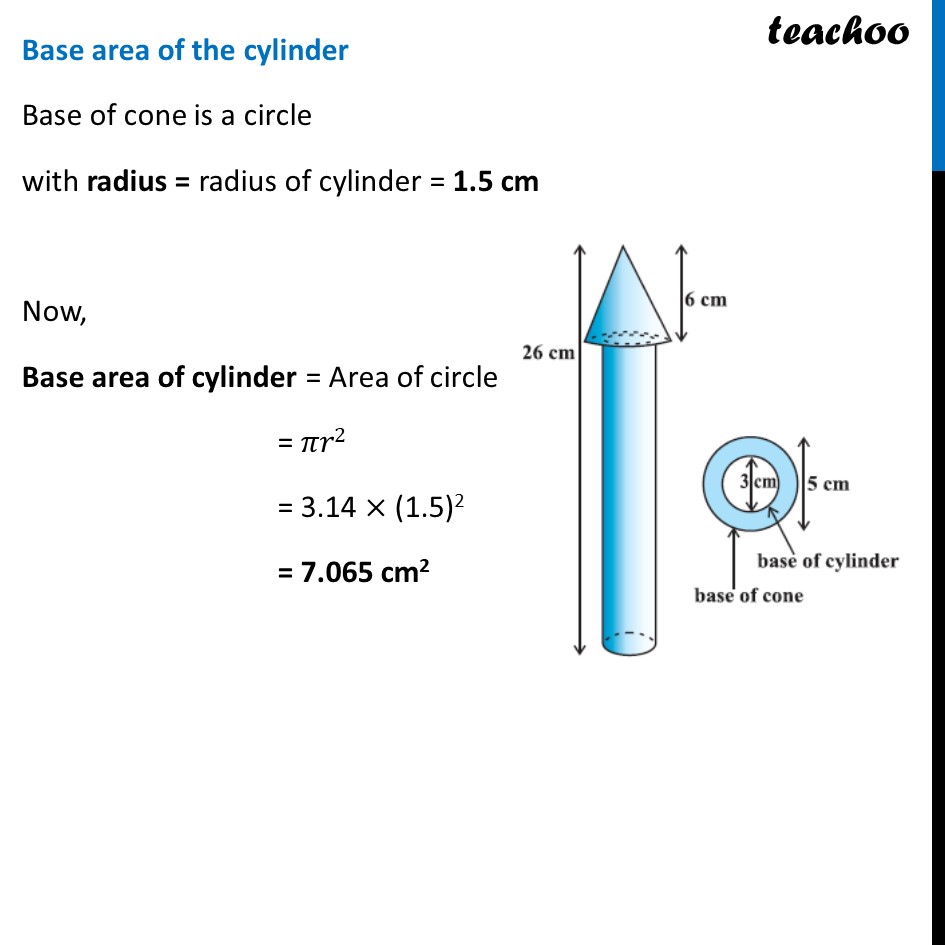
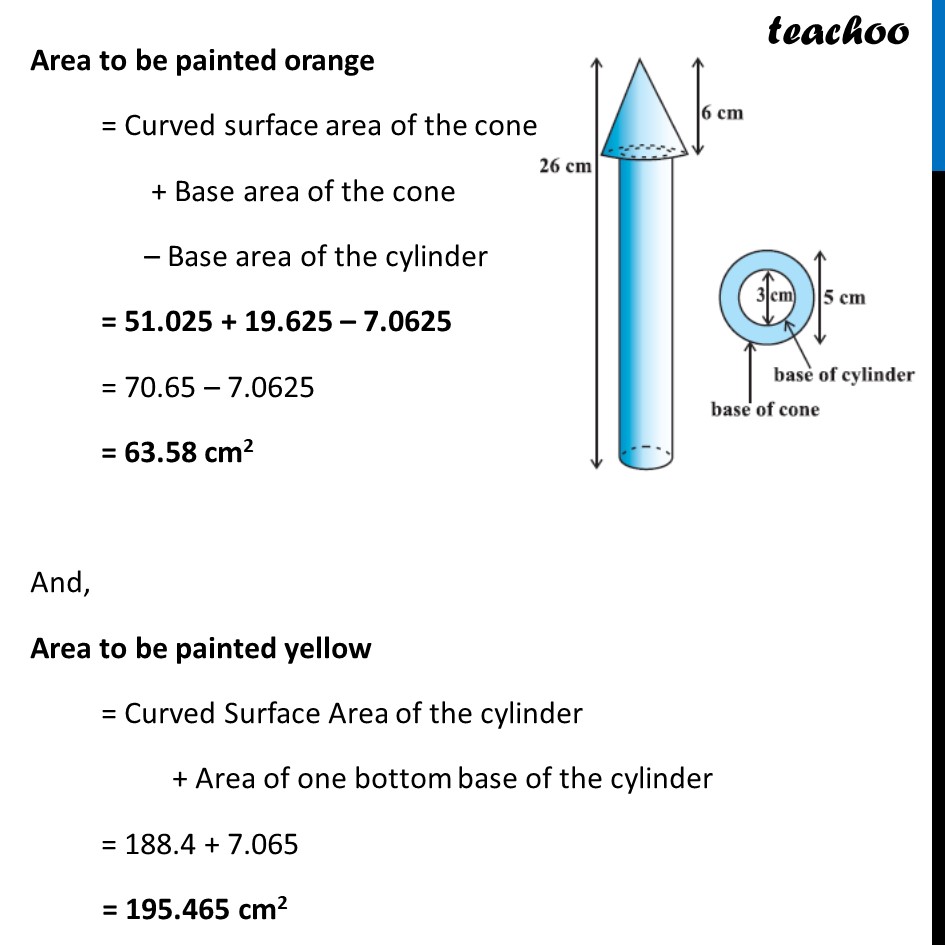
Example 3 A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π= 3.14) Now, Area to be painted orange = Curved surface area of the cone + Base area of the cone – Base area of the cylinder Area to be painted yellow = Curved Surface Area of the cylinder + Area of one bottom base of the cylinder Area to be painted yellow = Curved Surface Area of the cylinder + Area of one bottom base of the cylinder Curved surface area of the cone Curved Surface area of cone = 𝝅𝒓𝒍 Diameter of conical portion = 5 cm Radius of conical portion = r = 𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟/2 = 5/2 = 2.5 cm Height of the conical part = h = 6 cm We need to find 𝒍 first We know that l2 = h2 + r2 l2 = (6)2 + (5/2)^2 l2 = 36 + 25/4 l2 = (36(4) + 25)/4 l2 = 169/4 l = √(𝟏𝟔𝟗/𝟒) l = √(13^2/2^2 ) l = 𝟏𝟑/𝟐 l = 6.5 cm Curved Surface area of cone = 𝜋𝑟𝑙 = 3.14 × 2.5 × 6.5 = 51.025 cm2 Base area of the cone Base of cone is a circle with radius = radius of cone = 2.5cm Base area of cone = Area of circle = 𝜋𝑟2 = 3.14 × (2.5)2 = 3.14 × 6.25 = 19.625 cm2 Curved Surface area of the cylinder Diameter of cylinder = 3 cm Radius of cylinder = r = 𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟/2 = 3/2 = 1.5 cm Height of cylinder = Total height – Height of cone = 26 – 6 = 20 cm Now, Curved Surface area of the cylinder = 2𝜋𝑟h = 2 × 3.14 × 1.5 × 20 = 188.4 cm2 Base area of the cylinder Base of cone is a circle with radius = radius of cylinder = 1.5 cm Now, Base area of cylinder = Area of circle = 𝜋𝑟2 = 3.14 × (1.5)2 = 7.065 cm2 Area to be painted orange = Curved surface area of the cone + Base area of the cone – Base area of the cylinder = 51.025 + 19.625 – 7.0625 = 70.65 – 7.0625 = 63.58 cm2 And, Area to be painted yellow = Curved Surface Area of the cylinder + Area of one bottom base of the cylinder = 188.4 + 7.065 = 195.465 cm2