Ex 12.1, 4 - Chapter 13 Class 10 Surface Areas and Volumes (Important Question)

Transcript

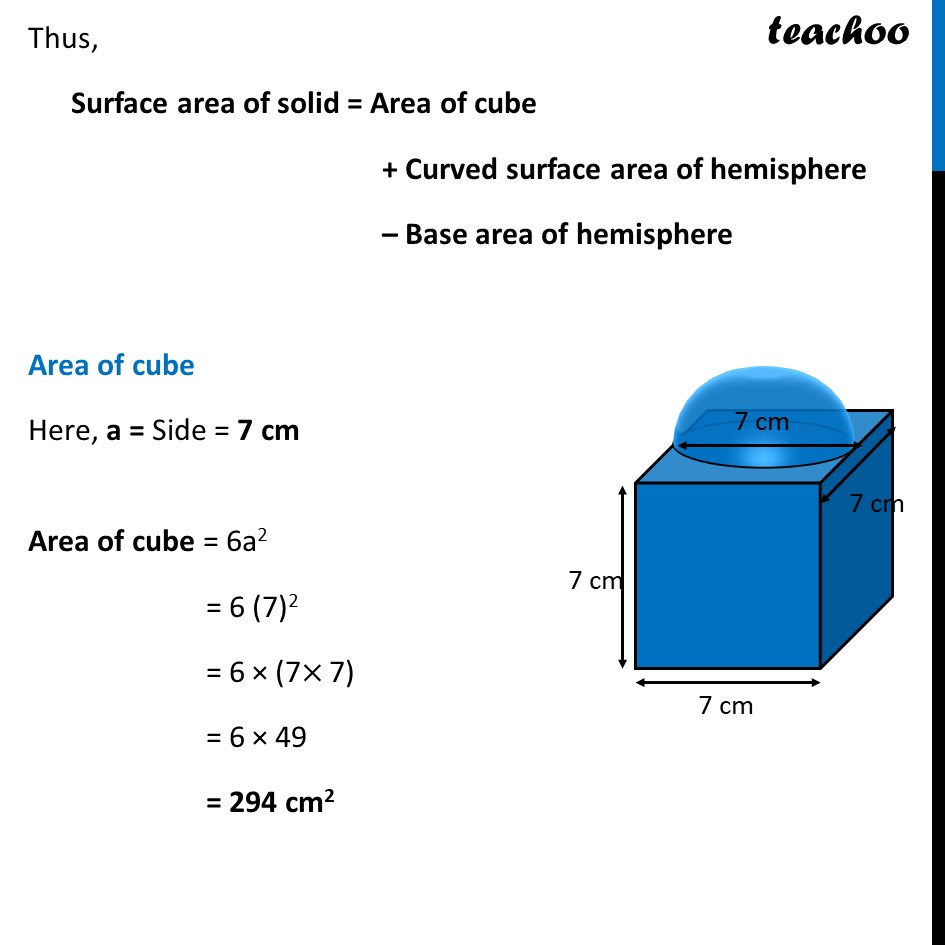
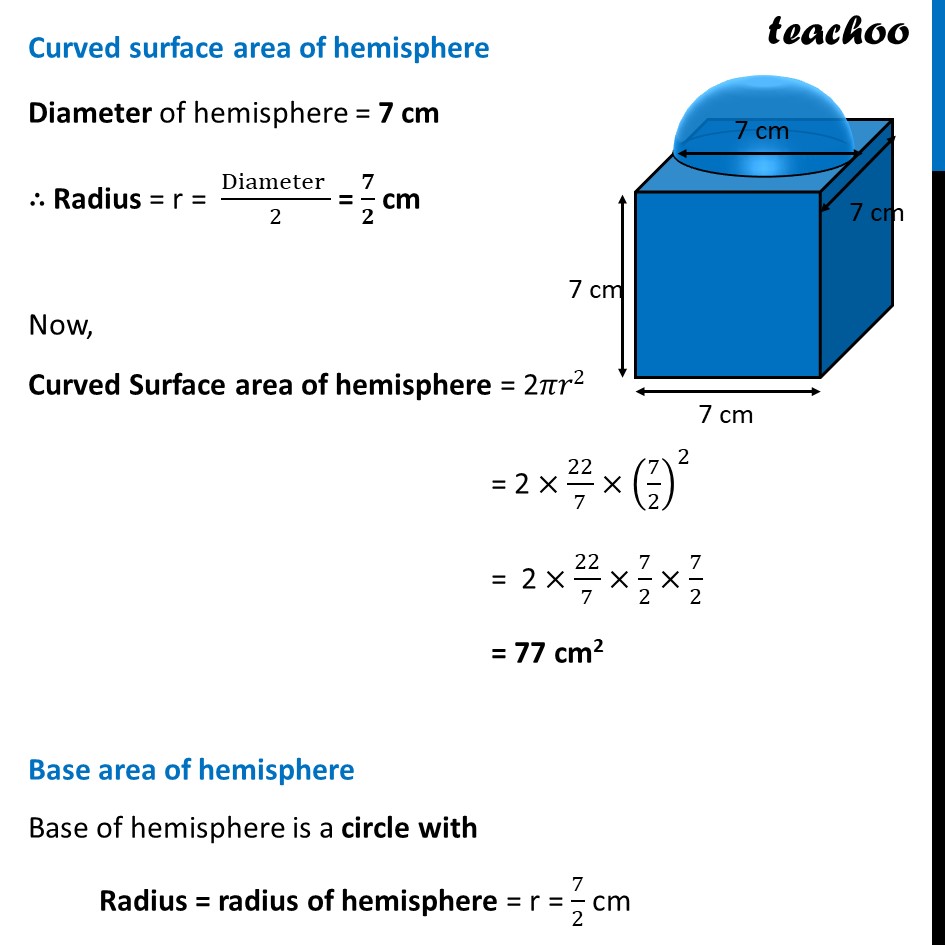
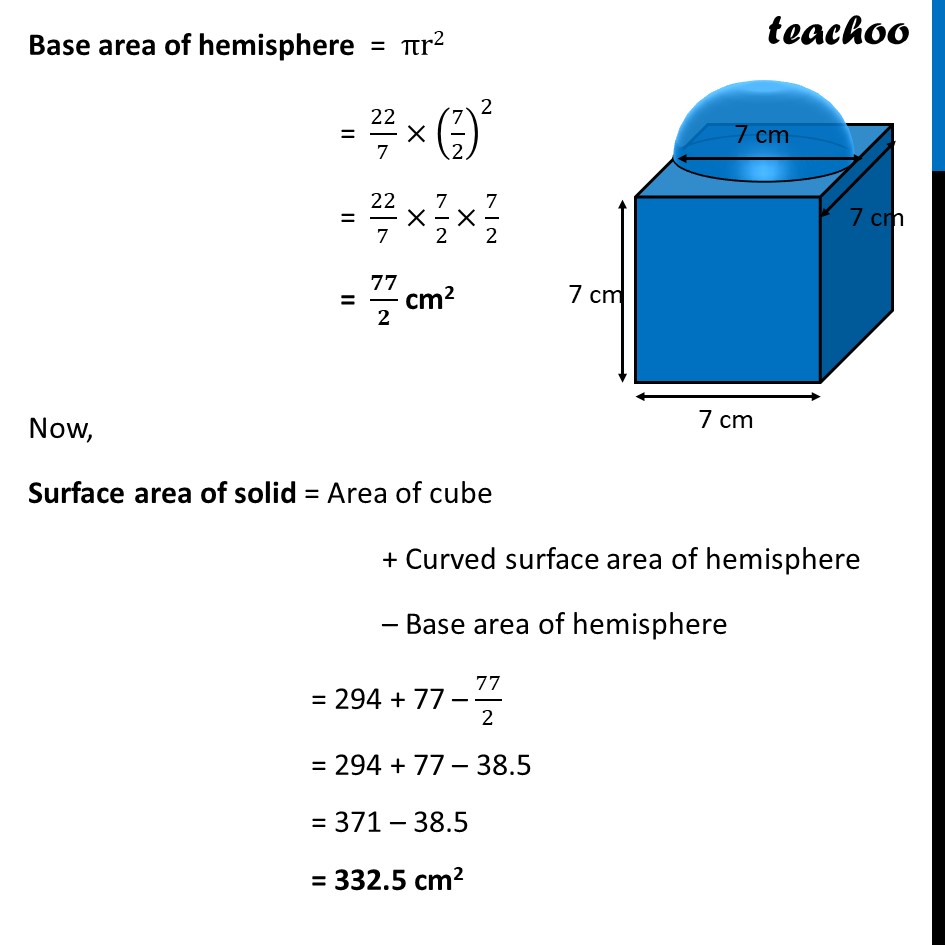
Ex 12.1, 4 A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid. The hemisphere can occupy whole of the side of cube. Hence, Greatest diameter of hemisphere = Side of cube = 7 cm Here, base of hemisphere falls on cube, so that Area should not from part of solid. Thus, Surface area of solid = Area of cube + Curved surface area of hemisphere – Base area of hemisphere Area of cube Here, a = Side = 7 cm Area of cube = 6a2 = 6 (7)2 = 6 × (7× 7) = 6 × 49 = 294 cm2 Curved surface area of hemisphere Diameter of hemisphere = 7 cm ∴ Radius = r = (Diameter )/2 = 𝟕/𝟐 cm Now, Curved Surface area of hemisphere = 2𝜋𝑟2 = 2 ×22/7×(7/2)^2 = 2 ×22/7×7/2×7/2 = 77 cm2 Base area of hemisphere Base of hemisphere is a circle with Radius = radius of hemisphere = r = 7/2 cm Base area of hemisphere = πr2 = 22/7×(7/2)^2 = 22/7×7/2×7/2 = 𝟕𝟕/𝟐 cm2 Now, Surface area of solid = Area of cube + Curved surface area of hemisphere – Base area of hemisphere = 294 + 77 – 77/2 = 294 + 77 – 38.5 = 371 – 38.5 = 332.5 cm2