Example 2 - Chapter 7 Class 10 Coordinate Geometry

Transcript

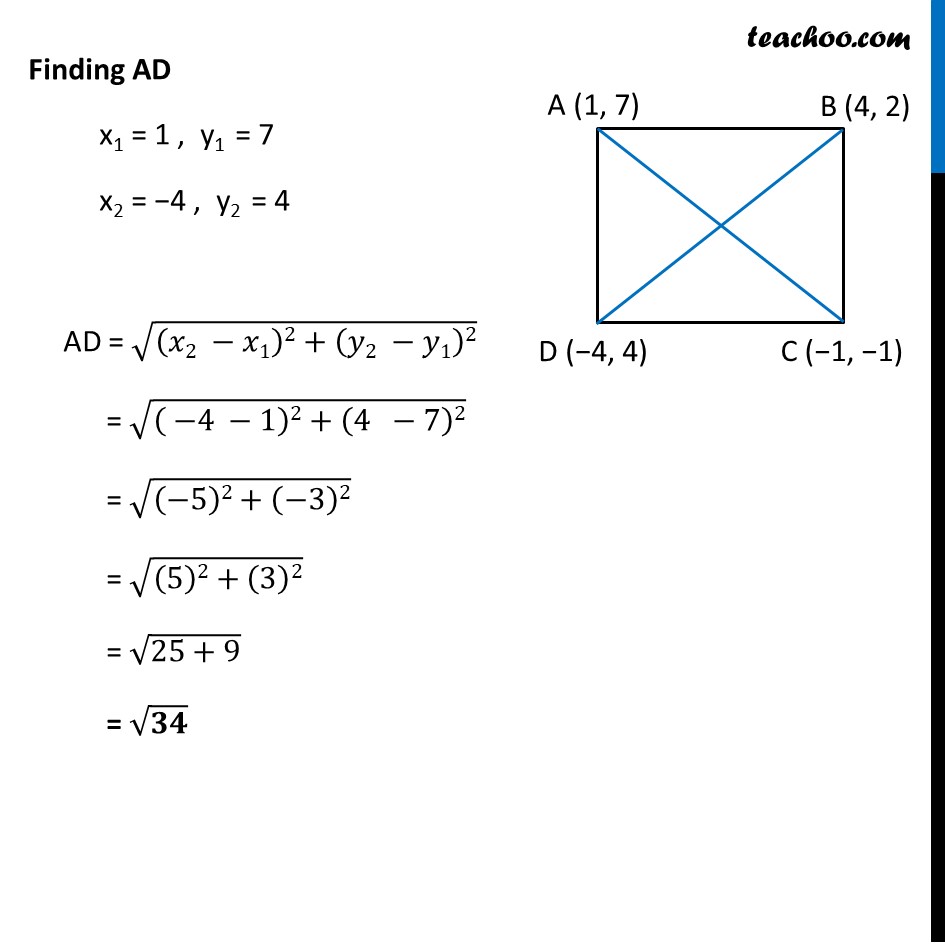
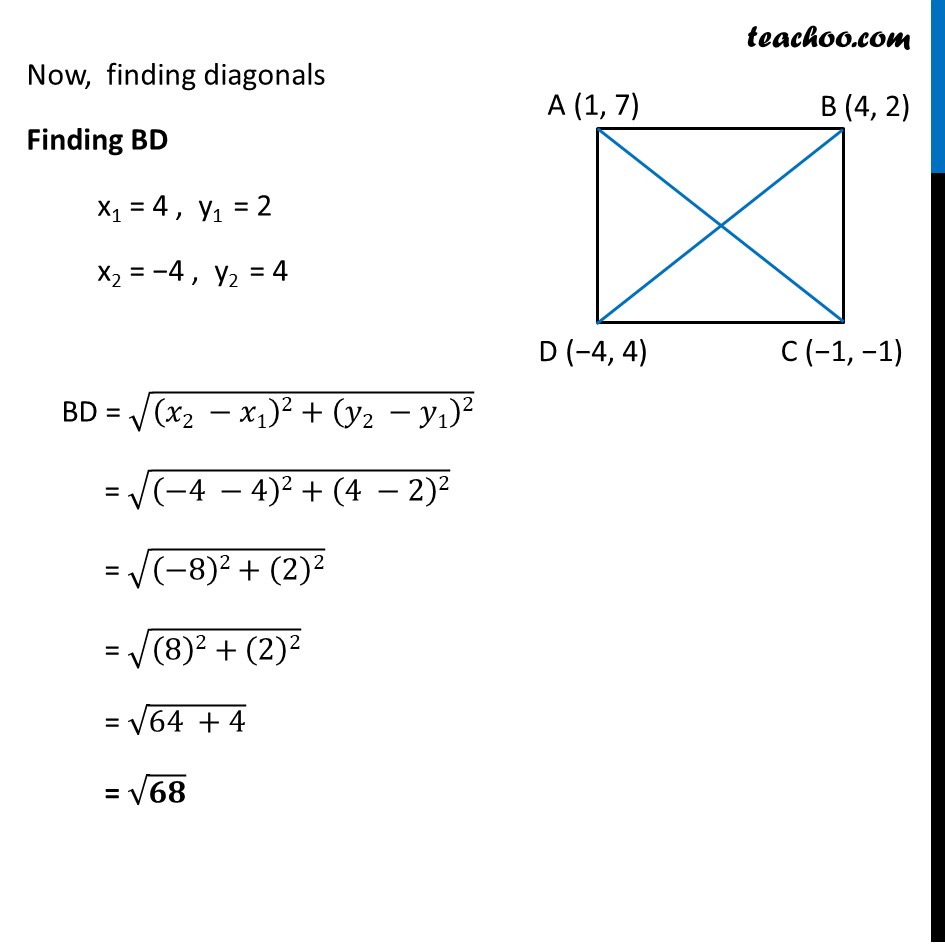
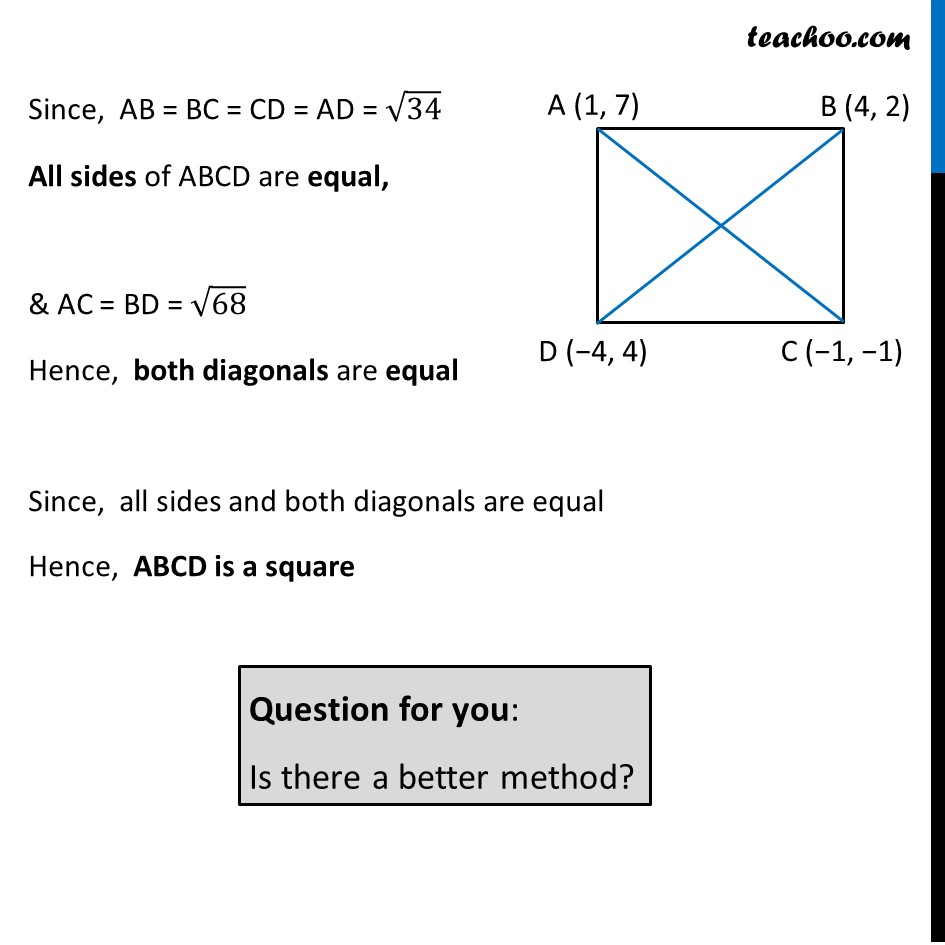
Example 2 Show that the points (1, 7), (4, 2), (–1, –1) and (– 4, 4) are the vertices of a square. Let the points be A(−1, −2), B(1, 0), C(−1, 2), D(−3, 0) To prove that ABCD is a square, We have to prove all sides equal, i.e. AB = BC = CD = AD & Diagonals equal i.e. AC = BD We find the distances AB, BC, CD & AD and AC & BD Finding AB x1 = 1 , y1 = 7 x2 = 4 , y2 = 2 AB = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √((4 −1)2+(2 −7)2) = √((3)2+(−5)2) = √((3)2+(5)2) = √(9+25) = √𝟑𝟒 Finding BC x1 = 4 , y1 = 2 x2 = −1 , y2 = −1 BC = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −1 −4)2+(−1 −2)2) = √((−5)2+(−3)2) = √((5)2+(3)2) = √(25+9) = √𝟑𝟒 Finding CD x1 = −1 , y1 = −1 x2 = −4 , y2 = 4 CD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −4 −(−1))2+(4 −(−1))2) = √((−4+1)2+(4+1)2) = √((−3)2+(5)2) = √((3)2+(5)2) = √(9+ 25) = √𝟑𝟒 Finding AD x1 = 1 , y1 = 7 x2 = −4 , y2 = 4 AD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −4 −1)2+(4 −7)2) = √((−5)2+(−3)2) = √((5)2+(3)2) = √(25+9) = √𝟑𝟒 Now, finding diagonals Finding AC x1 = 1 , y1 = 7 x2 = −1 , y2 = −1 AC = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −1 −1)2+(−1 −7)2) = √((−2)2+(−8)2) = √((2)2+(8)2) = √(4+64) = √𝟔𝟖 Now, finding diagonals Finding BD x1 = 4 , y1 = 2 x2 = −4 , y2 = 4 BD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √((−4 −4)2+(4 −2)2) = √((−8)2+(2)2) = √((8)2+(2)2) = √(64 +4) = √𝟔𝟖 Since, AB = BC = CD = AD = √34 All sides of ABCD are equal, & AC = BD = √68 Hence, both diagonals are equal Since, all sides and both diagonals are equal Hence, ABCD is a square Question for you: Is there a better method?