CBSE Class 12 Sample Paper for 2022 Boards (MCQ Based - for Term 1)
You are here
CBSE Class 12 Sample Paper for 2022 Boards (MCQ Based - for Term 1)
Last updated at Dec. 16, 2024 by Teachoo
This question is inspired from Misc 21 (MCQ) - Chapter 6 Class 12 - Application of Derivatives
Transcript
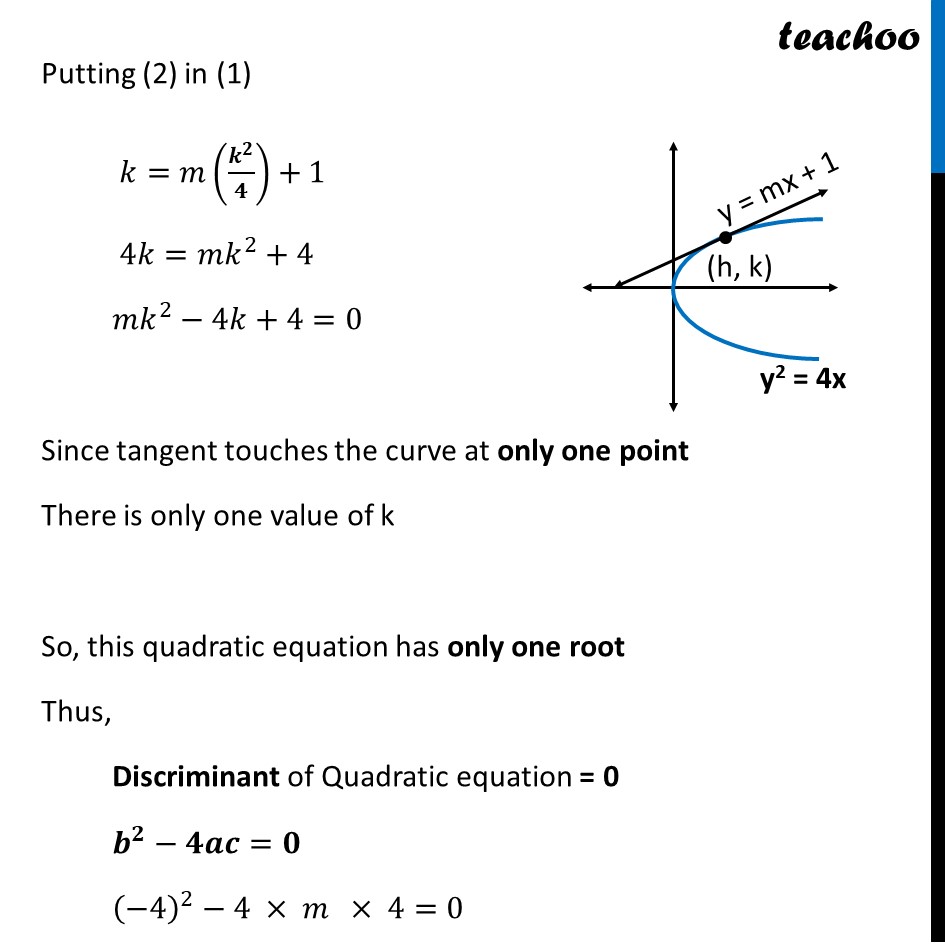
Question 42 For which value of m is the line y = mx + 1 a tangent to the curve y2 = 4x? (a) 1/2 (b) 1 (c) 2 (d) 3 Let (ℎ , 𝑘) be the point at which tangent is to be taken Since (𝒉 , 𝒌) lies on line 𝑘=𝑚ℎ+1 Since (𝒉 , 𝒌) lies on curve 𝑘^2=4ℎ ℎ=𝑘^2/4 Putting (2) in (1) 𝑘=𝑚(𝒌^𝟐/𝟒)+1 4𝑘=𝑚𝑘^2+4 𝑚𝑘^2−4𝑘+4=0 Since tangent touches the curve at only one point There is only one value of k So, this quadratic equation has only one root Thus, Discriminant of Quadratic equation = 0 𝒃^𝟐−𝟒𝒂𝒄=𝟎 (−4)^2−4 × 𝑚 × 4=0 16−16𝑚=0 𝑚=16/16 𝒎=𝟏 So, the correct answer is (B)
