Ex 9.3, 11 - Chapter 9 Class 9 Circles

Last updated at May 29, 2023 by

Ex 10.5, 11 - ABC and ADC are two right triangles with - Cyclic quadrilaterals

Ex 10.5, 11 - Chapter 10 Class 9 Circles - Part 2

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

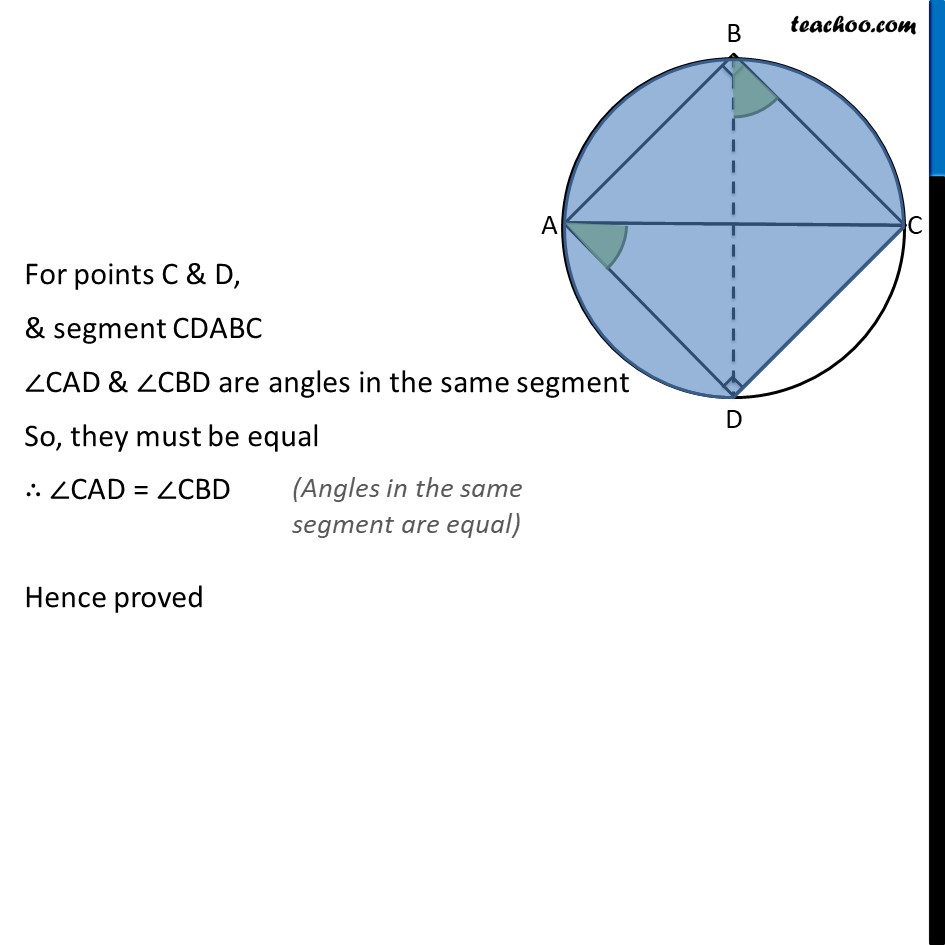
Ex 9.3, 11 ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD. Given: ∆ABC with ∠ B = 90° & ∆ADC with ∠ D = 90° To prove: ∠CAD = ∠CBD Proof: Considering quadrilateral ABCD ∠B + ∠D = 90° + 90° ⇒ ∠B + ∠D = 180° So, sum of one pair of opposite angles of quadrilateral ABCD is 180° ∴ ABCD is a cyclic quadrilateral We draw a circle in which ABCD is a cyclic quadrilateral We consider AC as diameter and draw a circle For points C & D, & segment CDABC ∠CAD & ∠CBD are angles in the same segment So, they must be equal ∴ ∠CAD = ∠CBD Hence proved

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.