Ex 9.3, 8 - Chapter 9 Class 9 Circles

Transcript

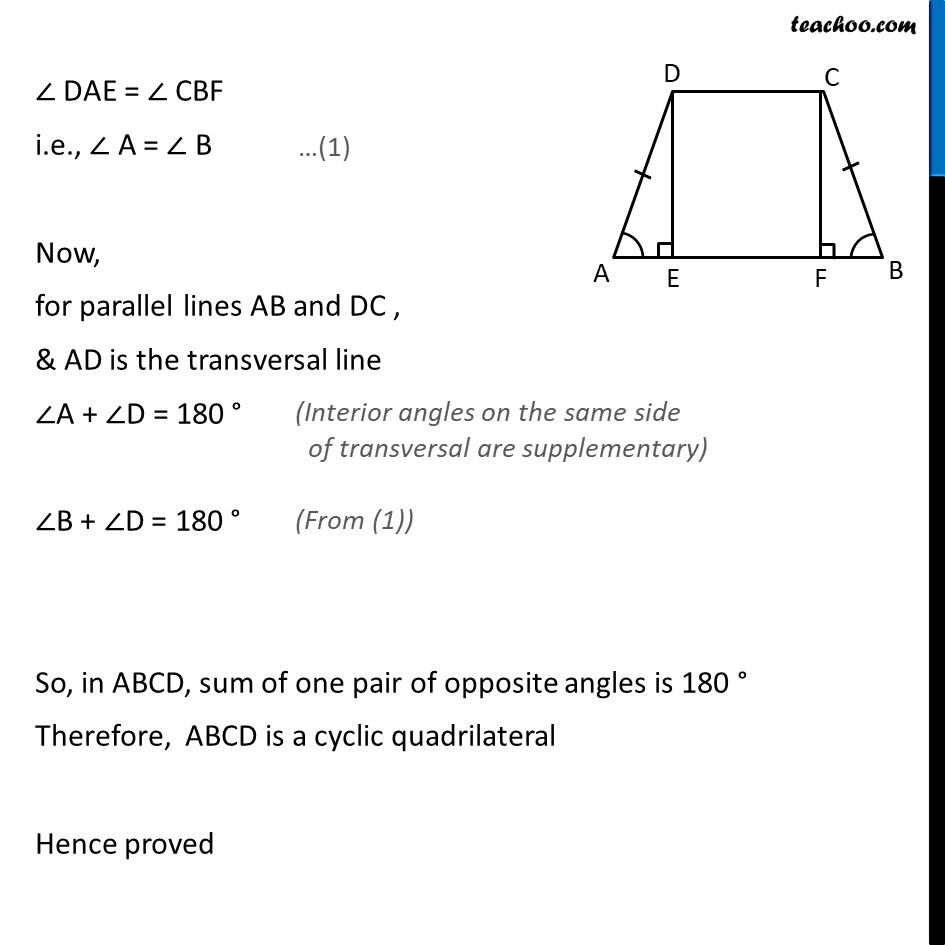
Ex 9.3, 8 If the non-parallel sides of a trapezium are equal, prove that it is cyclic. Given: ABCD is a trapezium where AB ∥ DC & non parallel sides are equal, i.e., AD = BC To prove: ABCD is cyclic quadrilateral Construction: We draw DE ⊥ AB & CF ⊥ AB Proof: To prove ABCD is a cyclic quadrilateral, we prove that sum of one pair of opposite angles is 180° In ∆ADE & ∆ BCF ∠AED = ∠ BFC AD = BC DE = CF ∴ ∆ADE ≅ ∆ BCF So, ∠ DAE = ∠ CBF i.e., ∠ A = ∠ B Now, for parallel lines AB and DC , & AD is the transversal line ∠A + ∠D = 180 ° ∠B + ∠D = 180 ° So, in ABCD, sum of one pair of opposite angles is 180 ° Therefore, ABCD is a cyclic quadrilateral Hence proved