
Last updated at Dec. 13, 2024 by Teachoo



Transcript
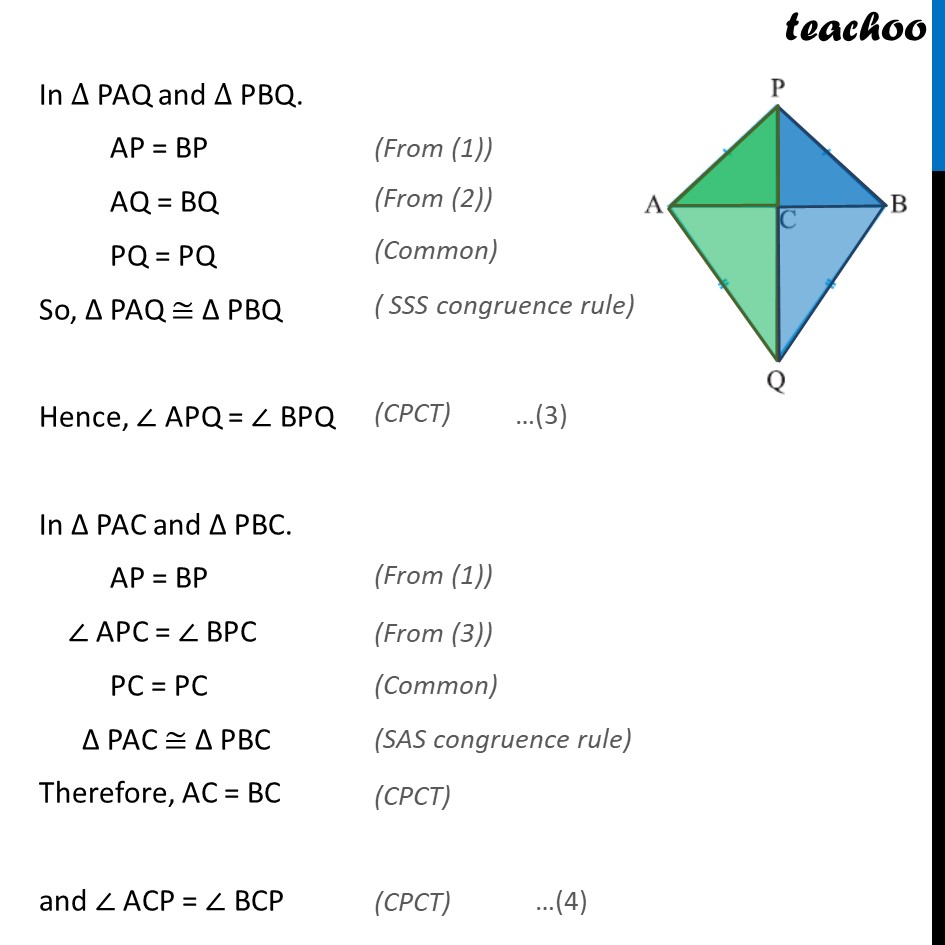
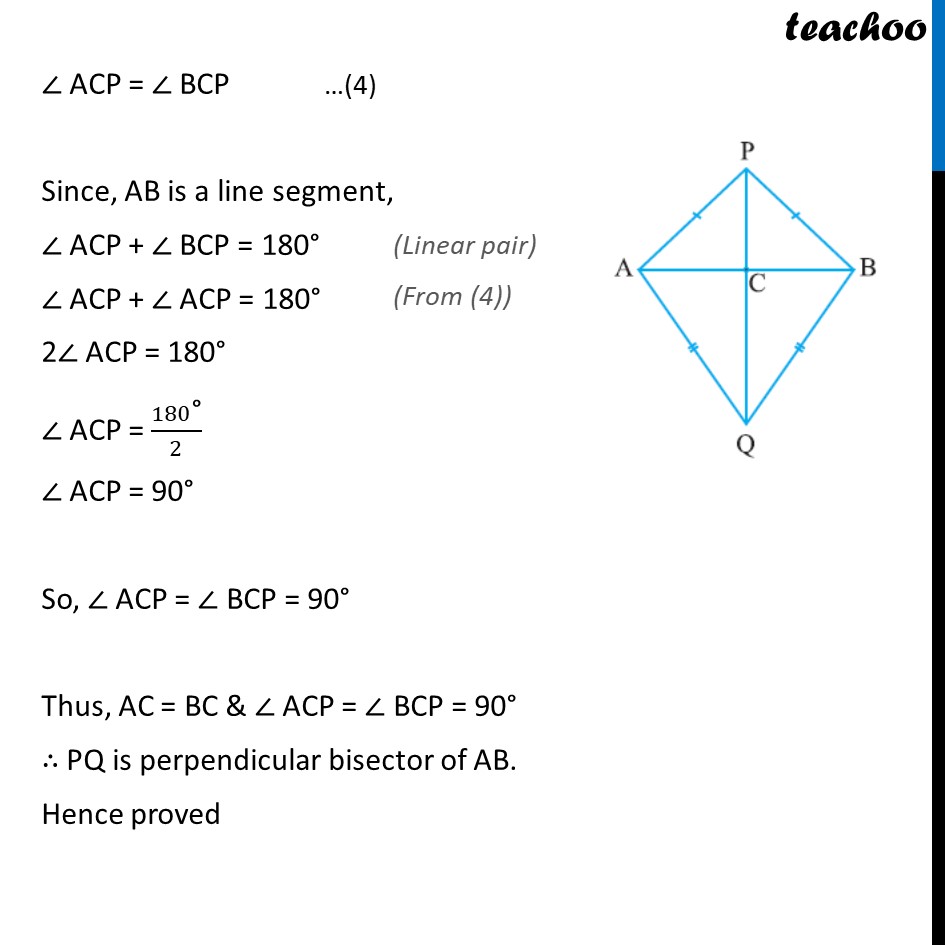
Example 7 AB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see figure). Show that the line PQ is the perpendicular bisector of AB. Given: P is equidistant from points A & B PA = PB and Q is equidistant from points A & B QA = QB To prove: PQ is perpendicular bisector of AB, i.e. AC = BC & ∠ PCA = ∠ PCB = 90° Proof : In ∆ PAQ and ∆ PBQ. AP = BP AQ = BQ PQ = PQ So, Δ PAQ ≅ Δ PBQ Hence, ∠ APQ = ∠ BPQ In Δ PAC and Δ PBC. AP = BP ∠ APC = ∠ BPC PC = PC Δ PAC ≅ Δ PBC Therefore, AC = BC and ∠ ACP = ∠ BCP ∠ ACP = ∠ BCP …(4) Since, AB is a line segment, ∠ ACP + ∠ BCP = 180° ∠ ACP + ∠ ACP = 180° 2∠ ACP = 180° ∠ ACP = 180"°" /2 ∠ ACP = 90° So, ∠ ACP = ∠ BCP = 90° Thus, AC = BC & ∠ ACP = ∠ BCP = 90° ∴ PQ is perpendicular bisector of AB. Hence proved