Question 1 - Important Triangle Questions - Chapter 7 Class 9 Triangles

Transcript

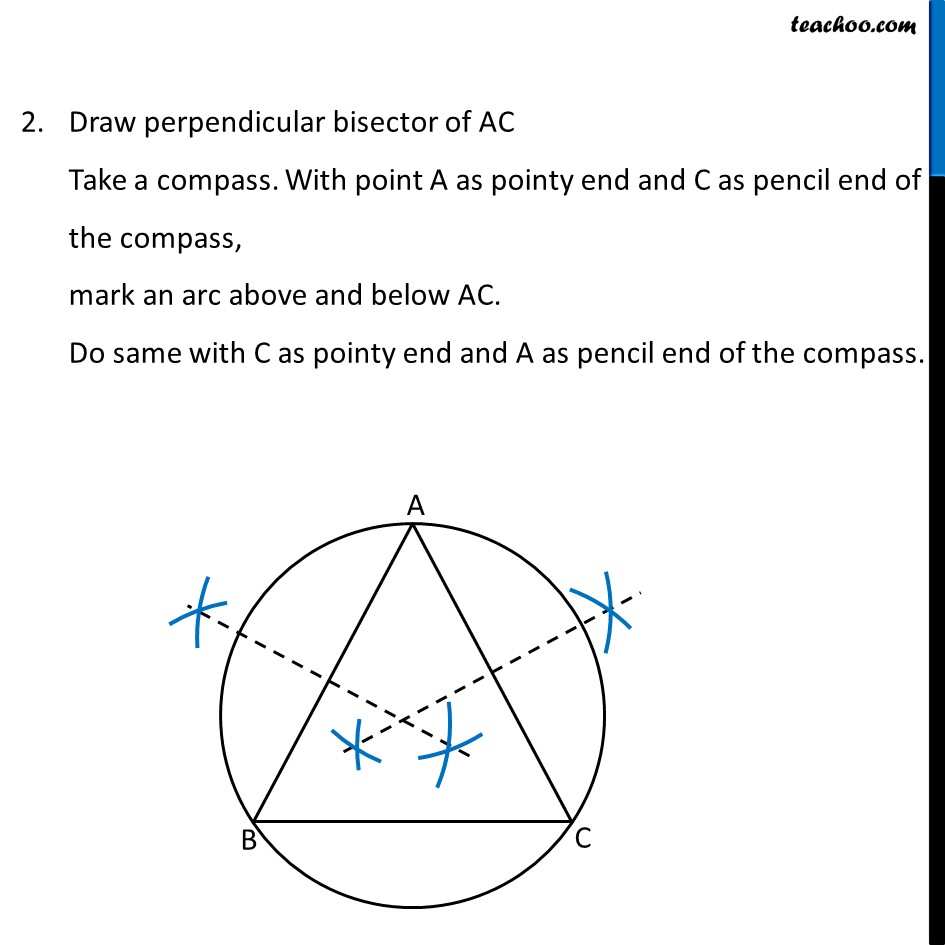
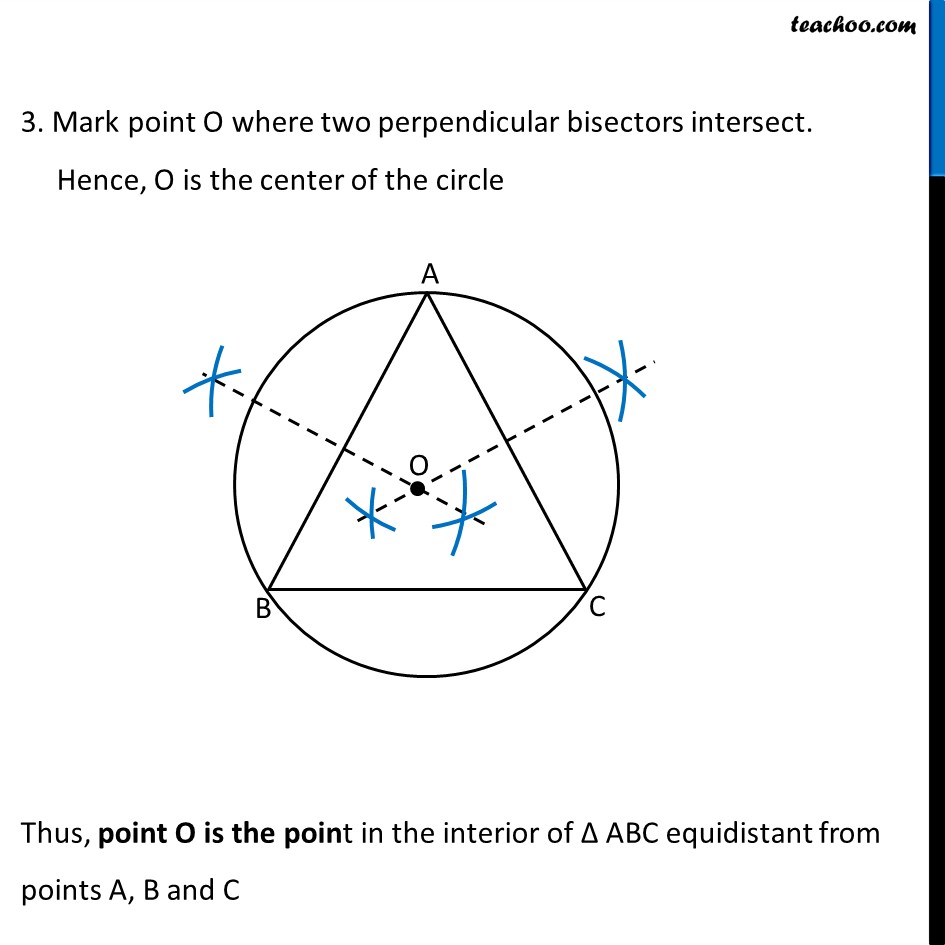
Question 1 ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of Δ ABC. An interior point which is equidistant from all the vertices of ∆ABC is its circumcentre Let’s draw a circle passing through points A, B, C So, Center of a circle will be equidistant from points A, B, C Center of circle will be the intersection of perpendicular bisector of sides of the triangle. Because perpendicular bisector of a chord passes through the center. Finding Center of circle Draw perpendicular bisector of AB Take a compass. With point A as pointy end and B as pencil end of the compass, mark an arc above and below AB. Do same with B as pointy end and A as pencil end of the compass. Draw perpendicular bisector of AC Take a compass. With point A as pointy end and C as pencil end of the compass, mark an arc above and below AC. Do same with C as pointy end and A as pencil end of the compass. 3. Mark point O where two perpendicular bisectors intersect. Hence, O is the center of the circle Thus, point O is the point in the interior of Δ ABC equidistant from points A, B and C