Question 1 - Angle opposite to longer side - Chapter 7 Class 9 Triangles

Transcript

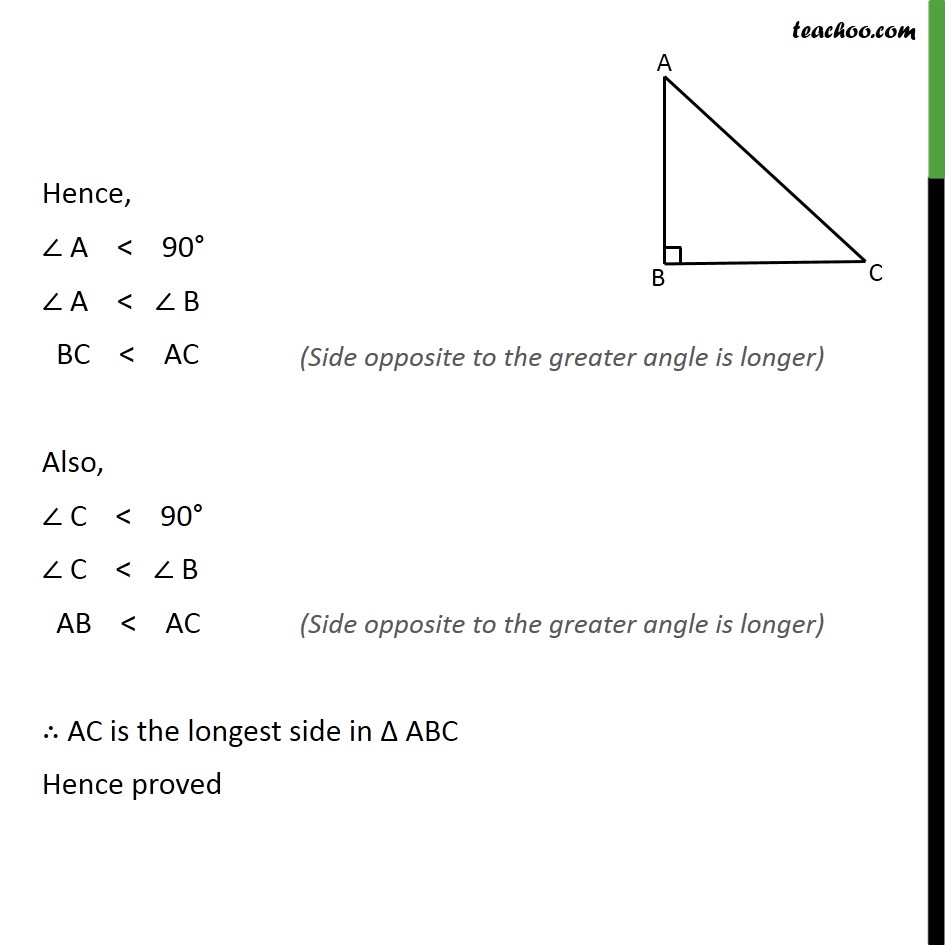
Ex7.4, 1 Show that in a right angled triangle, the hypotenuse is the longest side. Given: Δ ABC is a right-angled triangle , right-angled at B i.e. ∠ B = 90° To prove: AC is the longest side of ∆ ABC Proof: In ΔABC, ∠A + ∠B + ∠C = 180° ∠A + 90° + ∠C = 180° ∠A + ∠C = 180° – 90° ∠A + ∠C = 90° Angle can’t be 0 or negative Hence, ∠ A < 90° ∠ A < ∠ B BC < AC Also, ∠ C < 90° ∠ C < ∠ B AB < AC ∴ AC is the longest side in Δ ABC Hence proved