Ex 7.2, 1 - Chapter 7 Class 9 Triangles

Transcript

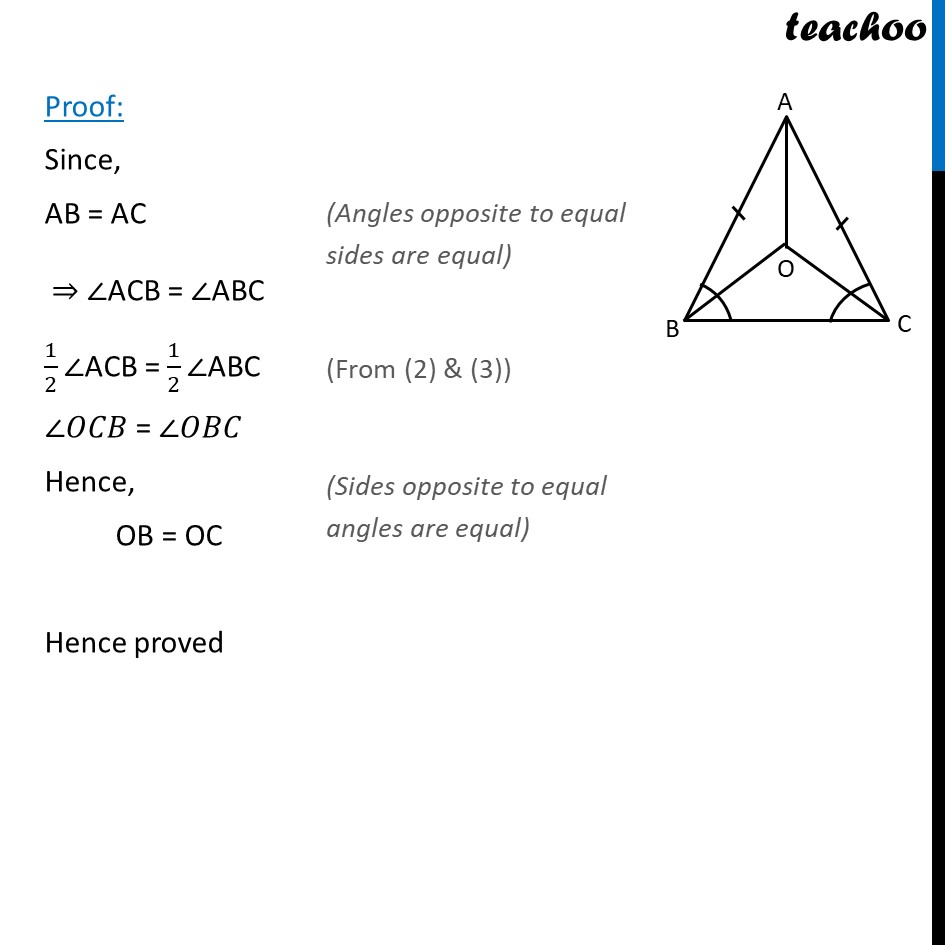
Ex 7.2,1 In an isosceles triangle ABC, with AB = AC the bisectors of ∠𝐵 and ∠C interest each other at O . Join A to O. show that : OB = OC Given: AB = AC OB is the bisector of ∠B So, ∠𝐴𝐵𝑂 = ∠𝑂𝐵𝐶 = 1/2 ∠𝐵 OC is the bisector of ∠C So, ∠𝐴𝐶𝑂 = ∠𝑂𝐶𝐵 = 1/2 ∠𝐶 To prove: OB = OC Proof: Since, AB = AC ⇒ ∠ACB = ∠ABC 1/2∠ACB = 1/2∠ABC ∠𝑂𝐶𝐵 = ∠𝑂𝐵𝐶 Hence, OB = OC Hence proved Ex 7.2,1 In an isosceles triangle ABC, with AB = AC the bisectors of ∠𝐵 and ∠𝐴 interest each other at O . Join A to O. show that : (ii) AO bisects ∠𝐴. To prove: ∠OAB= ∠OAC From part (i) OB = OC …(1) Also, In ∆ABO and ∆ACO, we have AB = AC AO = AO OB = OC ∴ ∆ ABO ≅ ∆ ACO ⇒ ∠𝑂𝐴𝐵 = ∠OAC Hence proved