Example 1 - Chapter 7 Class 9 Triangles

Transcript

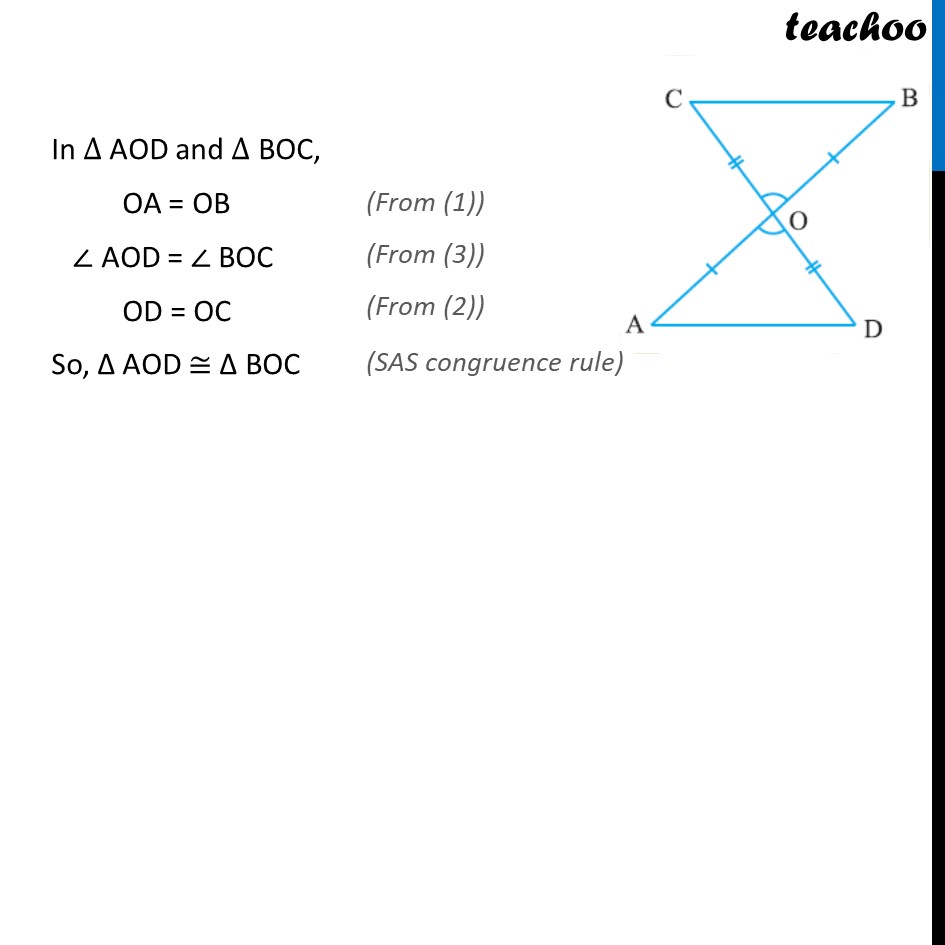
Example 1 - Chapter 7 Class 9 - Triangles In Fig. , OA = OB and OD = OC. Show that (i) ∆ AOD ≅ ∆ BOC Given: OA = OB ...(1) and OD = OC ...(2) To prove: ΔAOD ≅ ΔBOC Proof: Line CD & AB intersect. ∠ AOD = ∠ BOC (Vertically opposite angles) ...(3) In ∆ AOD and ∆ BOC, OA = OB (From (1)) ∠ AOD = ∠ BOC (From (3)) OD = OC (From (2)) So, Δ AOD ≅ Δ BOC (SAS Congruence Rule) Example 1 In Fig. , OA = OB and OD = OC. Show that (ii) AD ∥ BC. Δ AOD ≅ Δ BOC (From 1st part) ∠ OAD = ∠ OBC (CPCT) But ∠ OAD & ∠ OBC and these form a pair of alternate angles If a transversal intersects two lines such that pair of alternate interior angles is equal, then lines are parallel. Therefore, AD ∥ BC.