





Last updated at Feb. 24, 2025 by Teachoo







Transcript
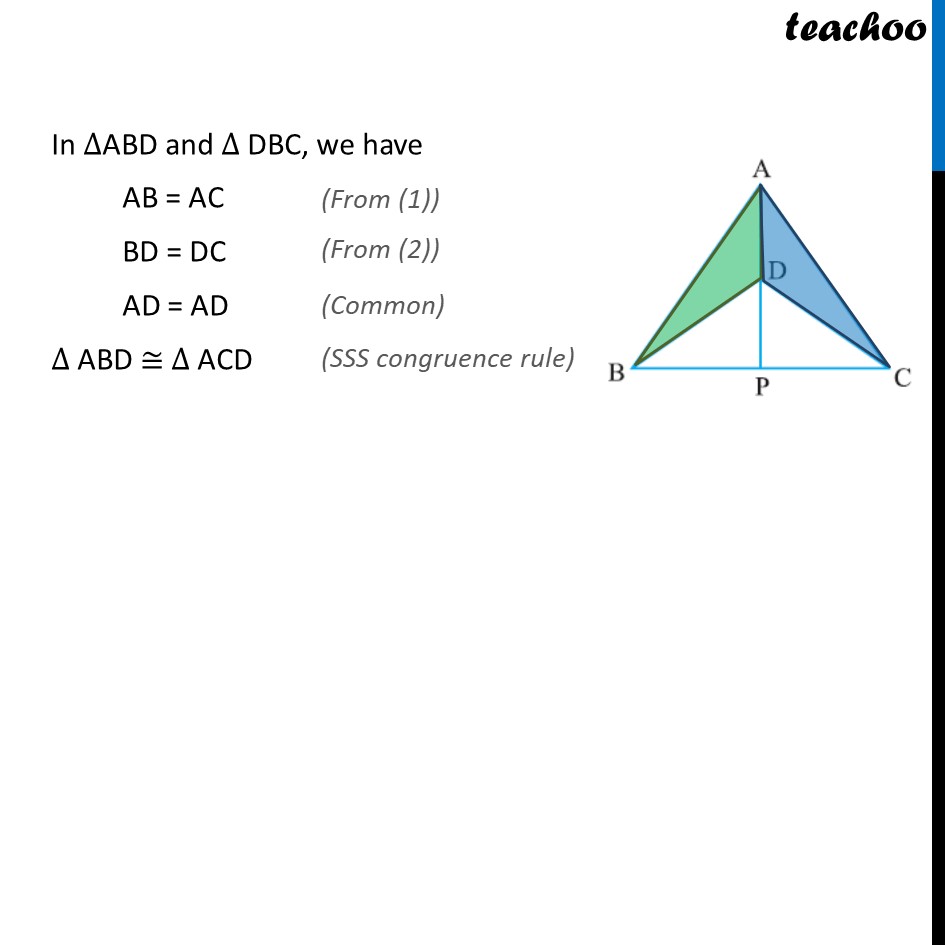
Ex 7.3,1 ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure ). If AD is extended to interest BC at P, show that ABD ACD Given: ABC is isosceles, AB = AC Also, DBC is isosceles, DB = DC To prove: ABD ACD Proof : In ABD and DBC, we have AB = AC BD = DC AD = AD ABD ACD Ex 7.3,1 ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure ). If AD is extended to interest BC at P, show that (ii) ABP ACP From part (i), ABD ACD So, BAP = PAC In ABP and ACP, AB = AC BAP = PAC AP = AP ABP ACP. Ex 7.3,1 ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure ). If AD is extended to interest BC at P, show that (iii)AP bisects as well as . To prove: = & = Proof: From part (i) , ABD ACD So, = . Hence AP bisects A For = , we will first prove BDP CDP From part(ii) , ABP ACP BP = CP In BDP and CDP, we have BD = CD BP = CP DP = DP So, BDP CDP = Thus, AP bisects D . Ex 7.3,1 ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure ). If AD is extended to interest BC at P, show that (iv) AP is the perpendicular bisector of BC To prove: BP = CP & = = 90 Proof From part(ii) , ABP ACP BP = CP = Since BC is a line, + = 180 + = 180 2 = 180 = (180 )/2 = 90 So, = = 90 Since, BP = CP & = = 90 AP is perpendicular bisector of BC.