Question 2 - Important Triangle Questions - Chapter 7 Class 9 Triangles

Transcript

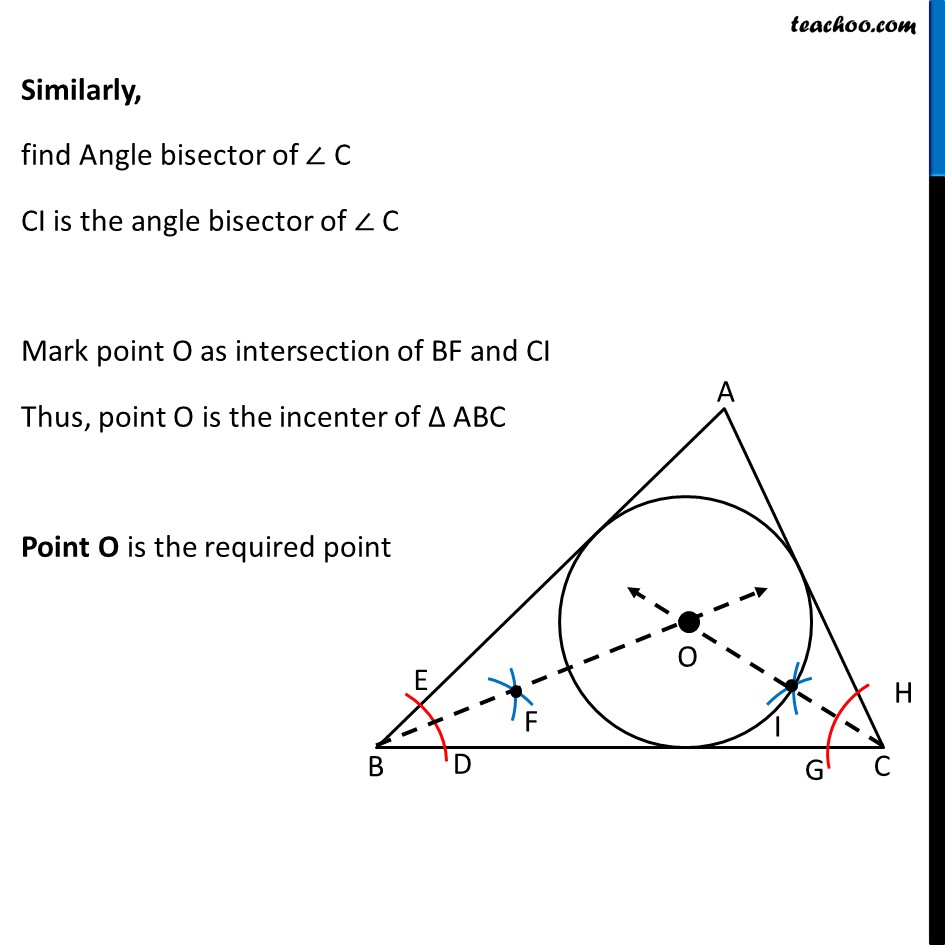
Question 2 In a triangle locate a point in its interior which is equidistant from all the sides of the triangle. An interior point in a triangle which is equidistant from all the sides is its incenter To locate the incenter of ∆ABC, We find intersection of its angle bisectors Finding Angle bisector of ∠ B Draw an arc of any radius intersecting BA and BC at points E & D Next, taking D and E as centers and with the radius more than 1/2 DE, draw arcs to intersect each other. 3. Mark the point as F. 4. Join BF So, BF is the bisector of the ∠ B Similarly, find Angle bisector of ∠ C CI is the angle bisector of ∠ C Mark point O as intersection of BF and CI Thus, point O is the incenter of Δ ABC Point O is the required point