Question 4 - Important Triangle Questions - Chapter 7 Class 9 Triangles

Transcript

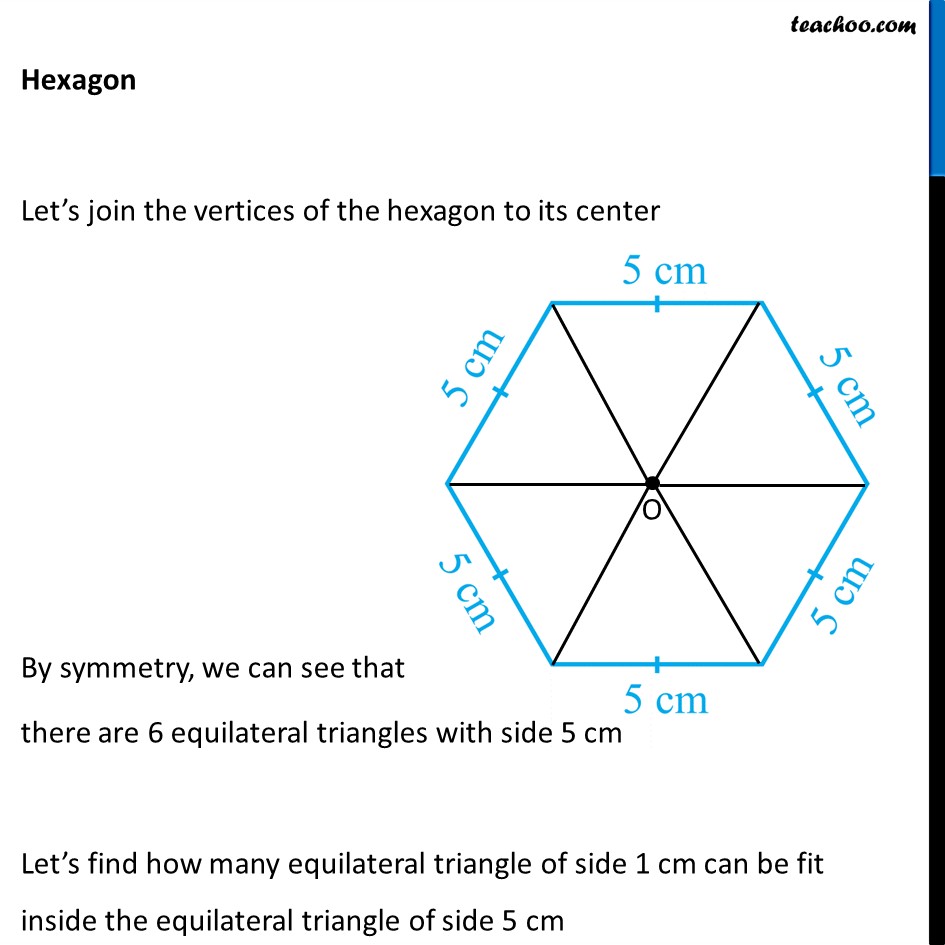
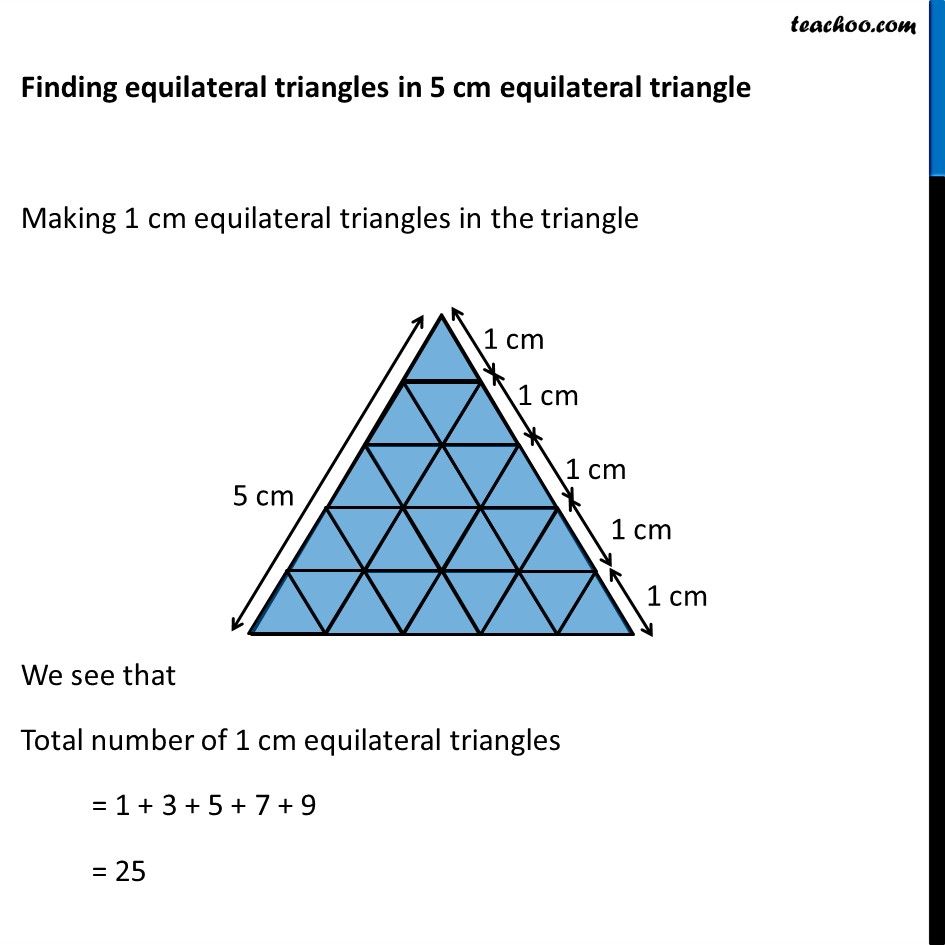
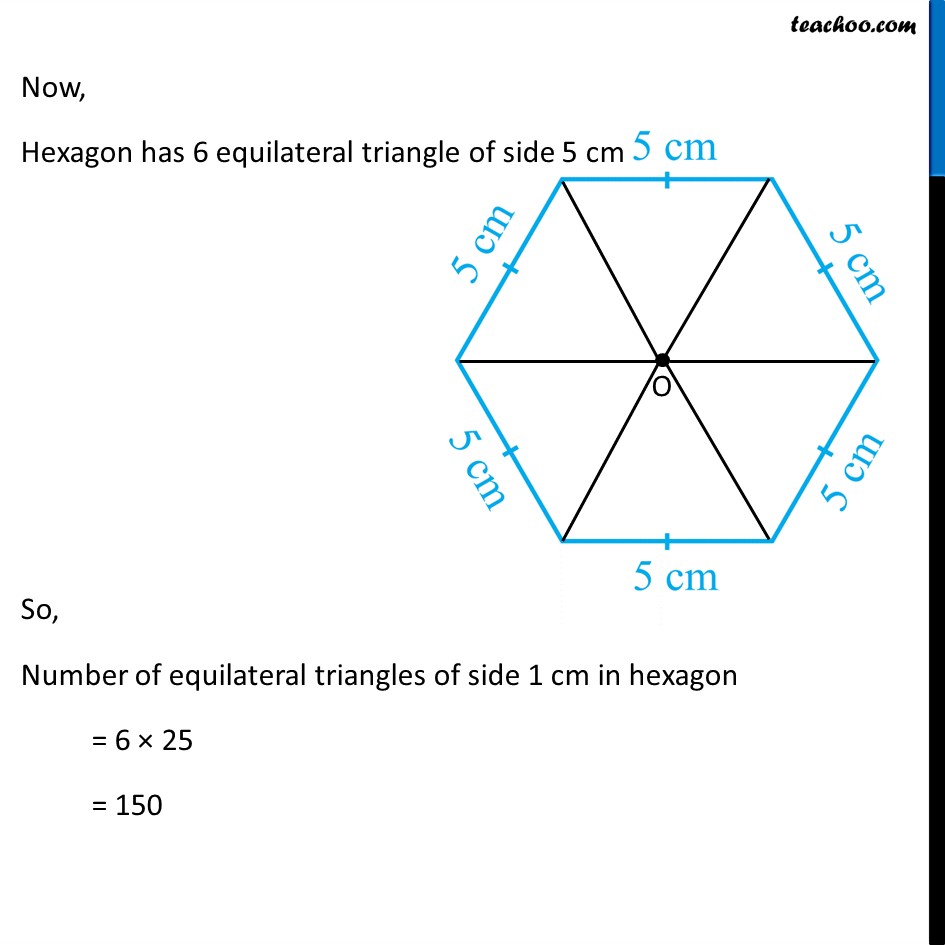
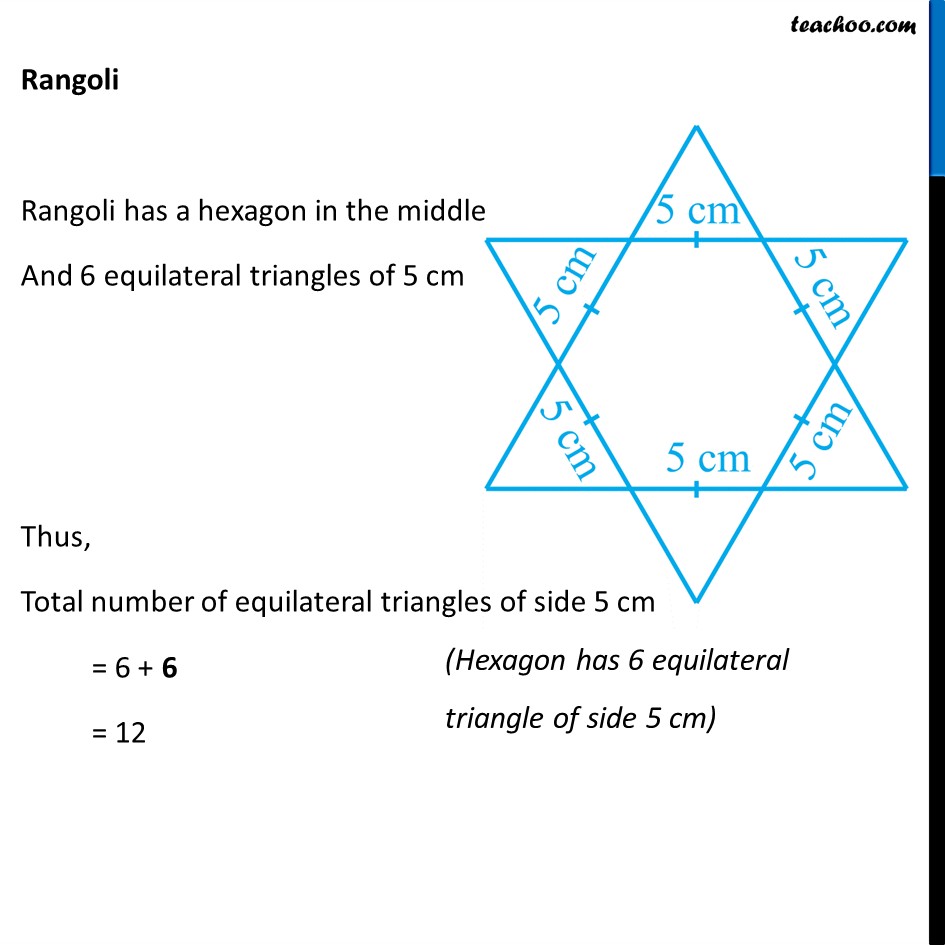
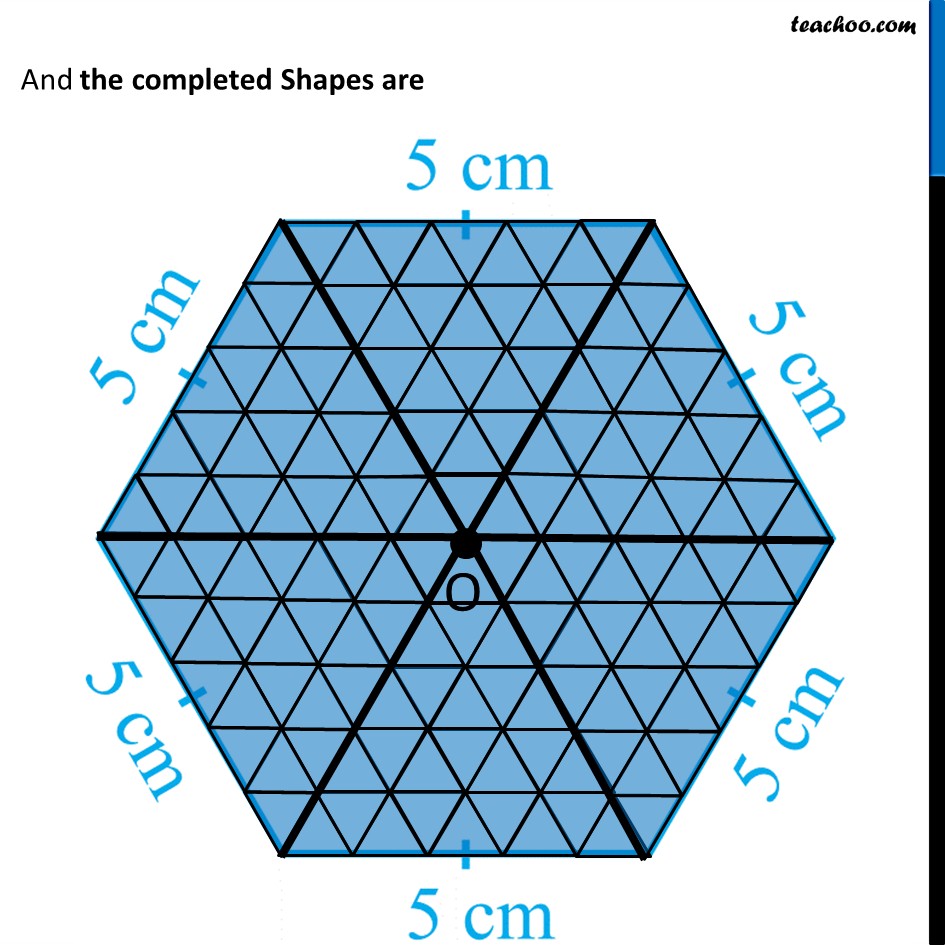
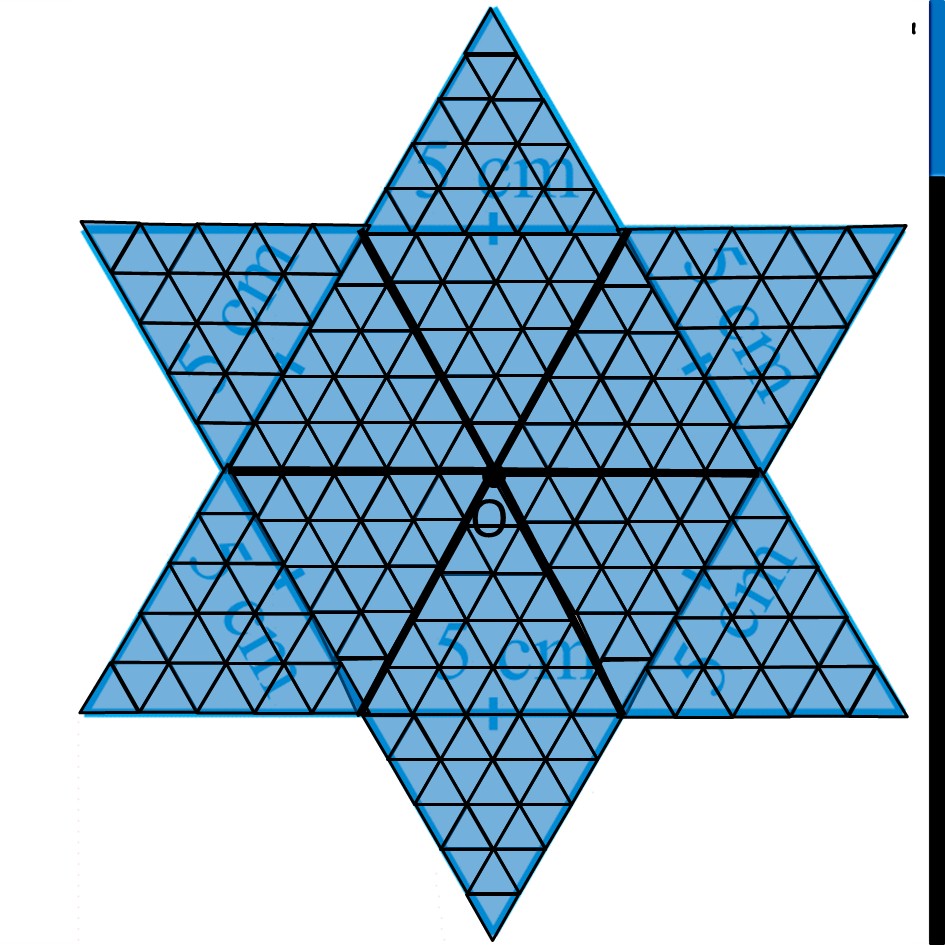
Question 4 Complete the hexagonal and star shaped Rangolies [See Fig 7.53 (i) and (ii) by filing them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles? Let’s look at the Hexagon first Hexagon Let’s join the vertices of the hexagon to its center By symmetry, we can see that there are 6 equilateral triangles with side 5 cm Let’s find how many equilateral triangle of side 1 cm can be fit inside the equilateral triangle of side 5 cm Finding equilateral triangles in 5 cm equilateral triangle Making 1 cm equilateral triangles in the triangle We see that Total number of 1 cm equilateral triangles = 1 + 3 + 5 + 7 + 9 = 25 We can also find number of triangles by area Area of 1 cm equilateral triangle = √3/4 (Side)2 Area of 1 cm equilateral triangle = √3/4 × 12 = √3/4 × 1 Area of 5 cm equilateral triangle = √3/4 × 52 = √3/4 × 25 Therefore, Number of 1 cm equilateral triangles = (𝐴𝑟𝑒𝑎 𝑜𝑓 5 𝑐𝑚 𝑒𝑞𝑢𝑖𝑙𝑎𝑡𝑒𝑟𝑎𝑙 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒)/(𝐴𝑟𝑒𝑎 𝑜𝑓 1 𝑐𝑚 𝑒𝑞𝑢𝑖𝑙𝑎𝑡𝑒𝑟𝑎𝑙 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒) = (√3/4 \ × 25)/(√3/4 \ × 1) = 25 Now, Hexagon has 6 equilateral triangle of side 5 cm So, Number of equilateral triangles of side 1 cm in hexagon = 6 × 25 = 150 Rangoli Rangoli has a hexagon in the middle And 6 equilateral triangles of 5 cm Thus, Total number of equilateral triangles of side 5 cm = 6 + 6 = 12 So, Number of equilateral triangles of side 1 cm in Rangoli = 12 × 25 = 300 So, Hexagon as 150 triangles Rangoli has 300 triangles