Question 5 - Chapter 7 Class 9 Triangles (Important Question)

Last updated at Dec. 13, 2024 by

Ex 7.4, 5 - In figure, PR > PQ and PS bisects ∠QPR - Ex 7.4

Ex 7.4, 5 - Chapter 7 Class 9 Triangles - Part 2

Go Ad-free

Transcript

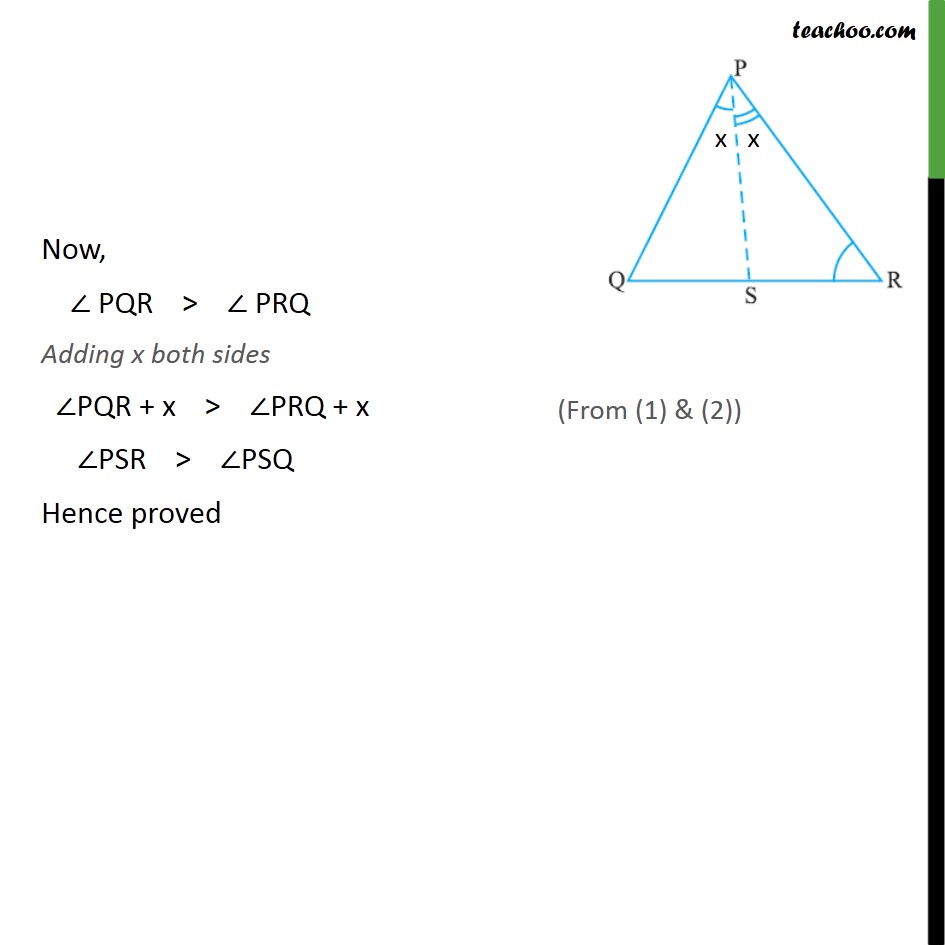
Ex7.4, 5 In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ. Given PR > PQ, ∴ ∠PQR > ∠PRQ PS is the bisector of ∠QPR. ∴ ∠QPS = ∠RPS Let ∠QPS = ∠RPS = x In Δ PQS, ∠PSR is the exterior angle ∠PSR = ∠PQR + x Now, ∠ PQR > ∠ PRQ Adding x both sides ∠PQR + x > ∠PRQ + x ∠PSR > ∠PSQ Hence proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo