Example 2 - Chapter 6 Class 9 Lines and Angles (Important Question)

Transcript

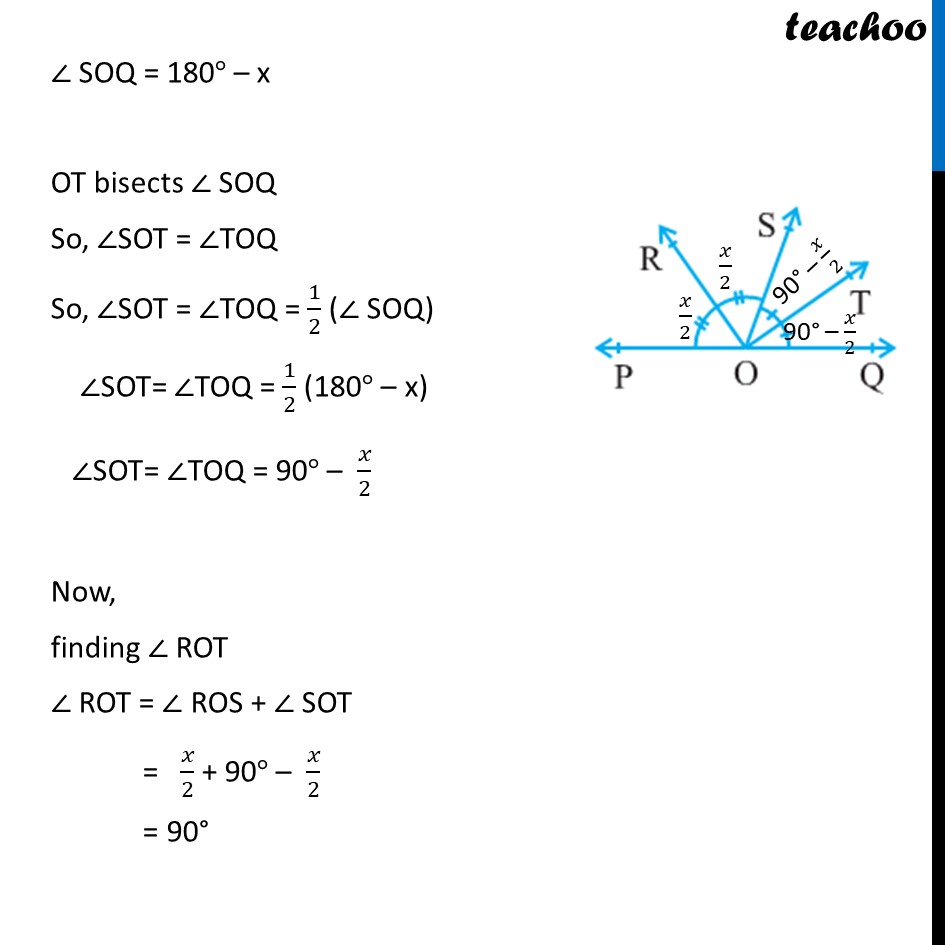
Example 2 In figure , ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠ POS and ∠ SOQ, respectively. If ∠ POS = x, find ∠ ROT. Given ∠ POS = x OR bisects ∠ POS So, ∠ROP = ∠ROS So, ∠ROP = ∠ROS = 1/2 (∠ POS) ∠ROP = ∠ROS = 𝑥/2 Now, ∠POS + ∠ SOQ = 180° x + ∠ SOQ = 180° ∠SOQ = 180° – x OT bisects ∠ SOQ So, ∠SOT = ∠TOQ So, ∠SOT = ∠TOQ = 1/2 (∠ SOQ) ∠SOT= ∠TOQ = 1/2 (180° – x) ∠SOT= ∠TOQ = 90° – 𝑥/2 Now, finding ∠ ROT ∠ ROT = ∠ ROS + ∠ SOT = 𝑥/2 + 90° – 𝑥/2 = 90°