Example 4 - Chapter 8 Class 9 Quadrilaterals (Important Question)

Transcript

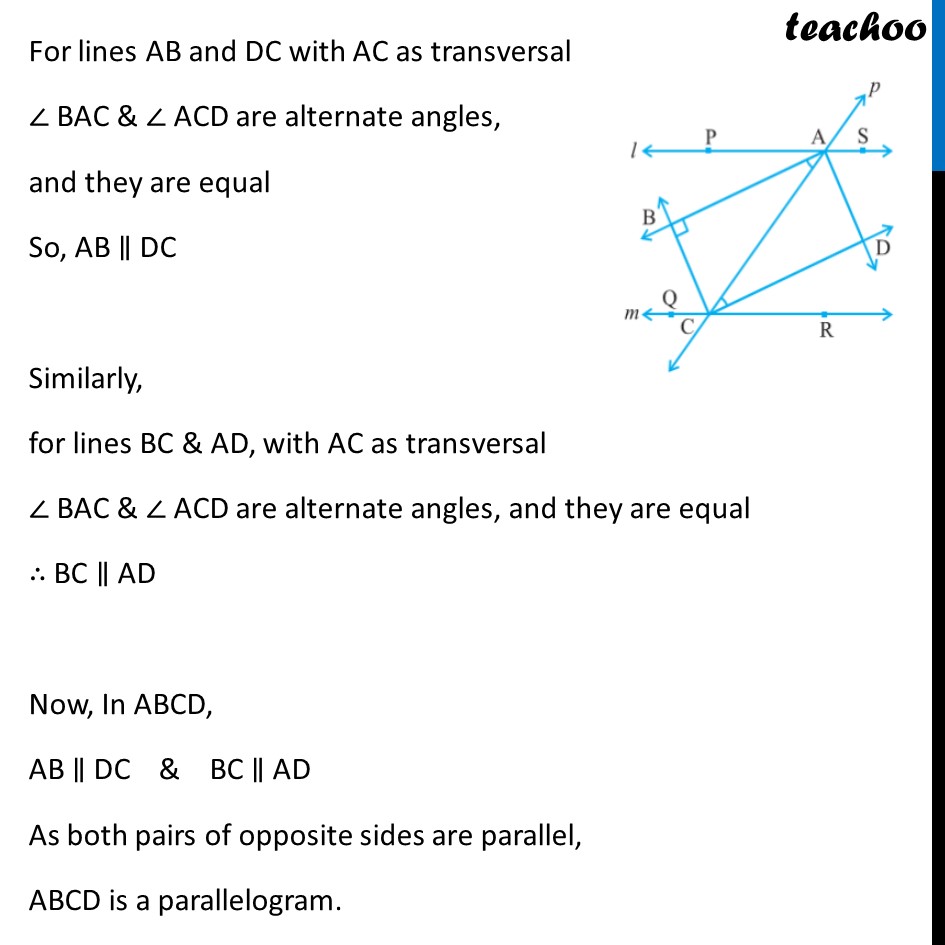
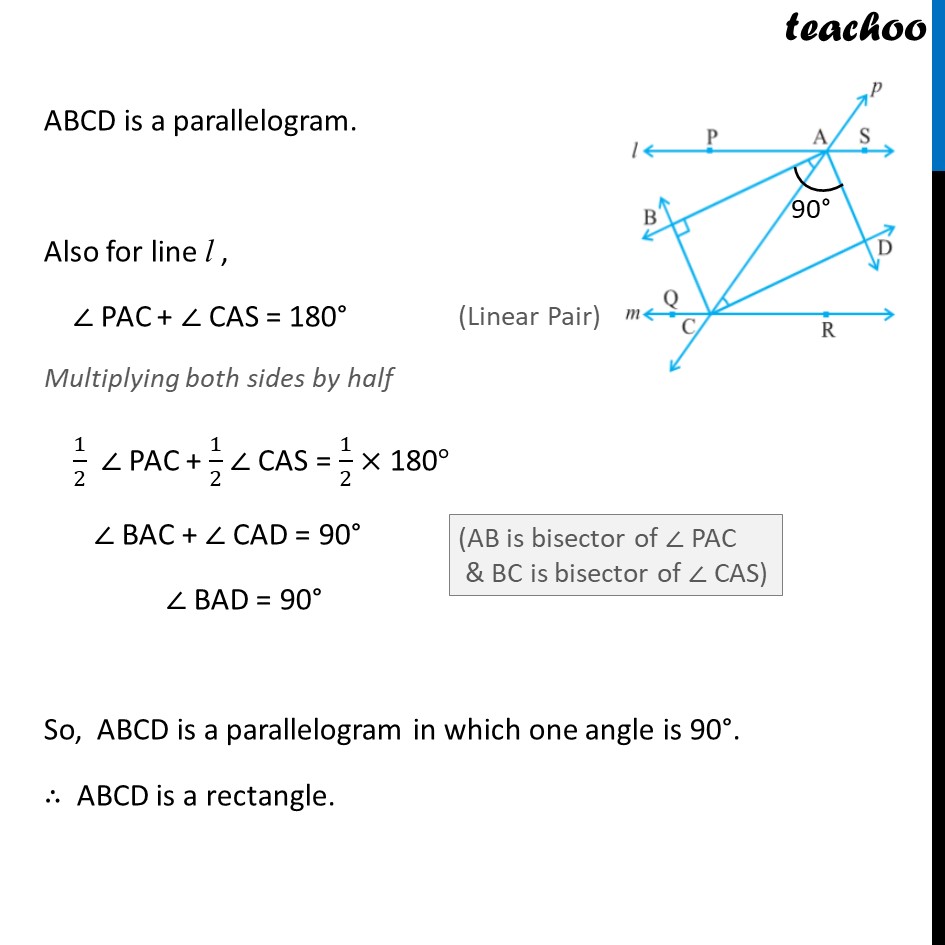
Example 4 Two parallel lines l and m are intersected by a transversal p. Show that the quadrilateral formed by the bisectors of interior angles is a rectangle. Given: line l ∥ m transversal p intersects l & m at A & C resp. Bisector of ∠ PAC & ∠QCA meet at B & Bisector of ∠ SAC & ∠RCA meet at D To prove: ABCD is a rectangle Proof: We know that a rectangle is a parallelogram with one angle 90° First we will prove ABCD is a parallelogram, For l ∥ m & transversal p ∠ PAC = ∠ ACR So ,1/2 ∠ PAC = 1/2 ∠ ACR i.e., ∠ BAC = ∠ ACD For lines AB and DC with AC as transversal ∠ BAC & ∠ ACD are alternate angles, and they are equal So, AB ∥ DC Similarly, for lines BC & AD, with AC as transversal ∠ BAC & ∠ ACD are alternate angles, and they are equal ∴ BC ∥ AD Now, In ABCD, AB ∥ DC & BC ∥ AD As both pairs of opposite sides are parallel, ABCD is a parallelogram. Also for line l , ∠ PAC + ∠ CAS = 180° Multiplying both sides by half 1/2 ∠ PAC + 1/2 ∠ CAS = 1/2 × 180° ∠ BAC + ∠ CAD = 90° ∠ BAD = 90° So, ABCD is a parallelogram in which one angle is 90°. ∴ ABCD is a rectangle.