Question 2 - Chapter 9 Class 9 Areas of parallelograms and Triangles (Important Question)

Transcript

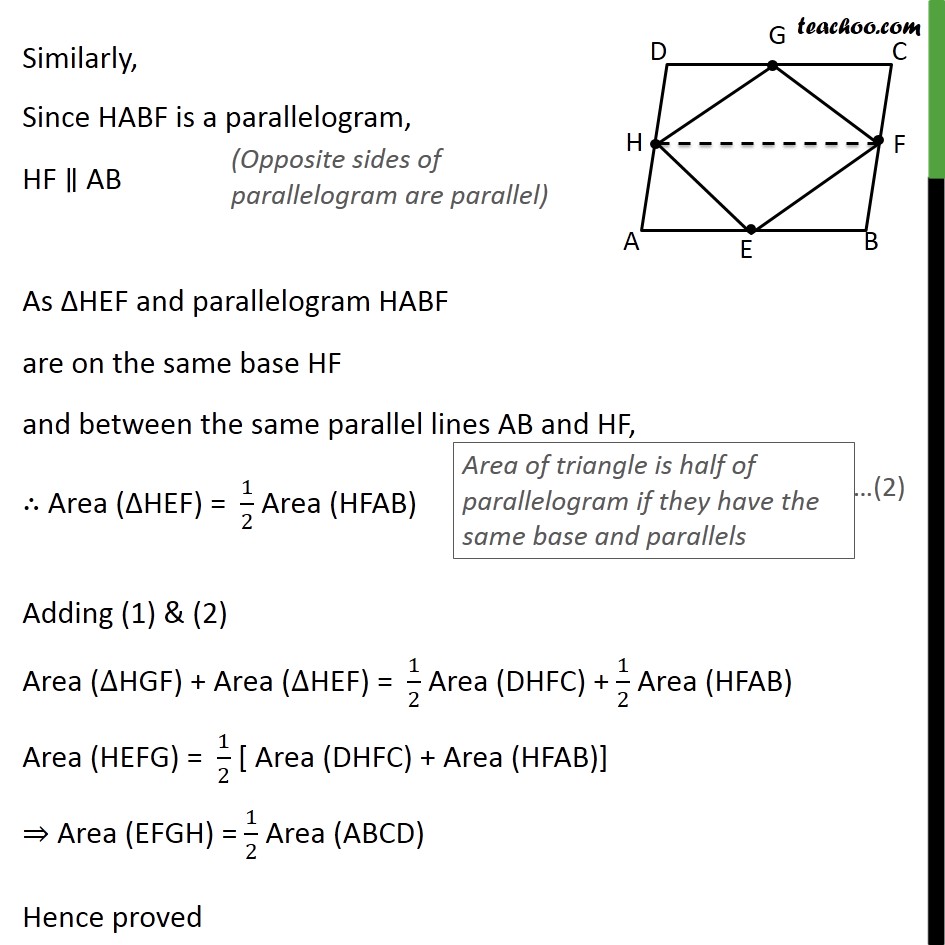
Question 2 If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD show that ar (EFGH) = 1/2 ar (ABCD) Given: A parallelogram ABCD where E, F, G, H are the mid-points of AB,BC,CD & AD respectively To prove: ar (EFGH) = 1/2 ar (ABCD) Proof: Join H & F Now, So, AD ∥ BC ⇒ DH ∥ CF Also, AD = BC 1/2 AD = 1/2 BC DH = CF In DHFC, DH = CF & DH ∥ CF ‖ Since one pair of opposite sides are equal and parallel ∴ DHFC is a parallelogram Similarly, HABF is a parallelogram Since DHFC is a parallelogram, DC ∥ HF As ΔHGF and parallelogram DHFC are on the same base HF & between the same parallel lines DC and HF, ∴ Area (ΔHGF) = 1/2 Area (DHFC) Similarly, Since HABF is a parallelogram, HF ∥ AB As ΔHEF and parallelogram HABF are on the same base HF and between the same parallel lines AB and HF, ∴ Area (ΔHEF) = 1/2 Area (HFAB) Adding (1) & (2) Area (∆HGF) + Area (∆HEF) = 1/2 Area (DHFC) + 1/2 Area (HFAB) Area (HEFG) = 1/2 [ Area (DHFC) + Area (HFAB)] ⇒ Area (EFGH) = 1/2 Area (ABCD) Hence proved