Question 4 (iii) - Cross Multiplication Method - Chapter 3 Class 10 Pair of Linear Equations in Two Variables

Transcript

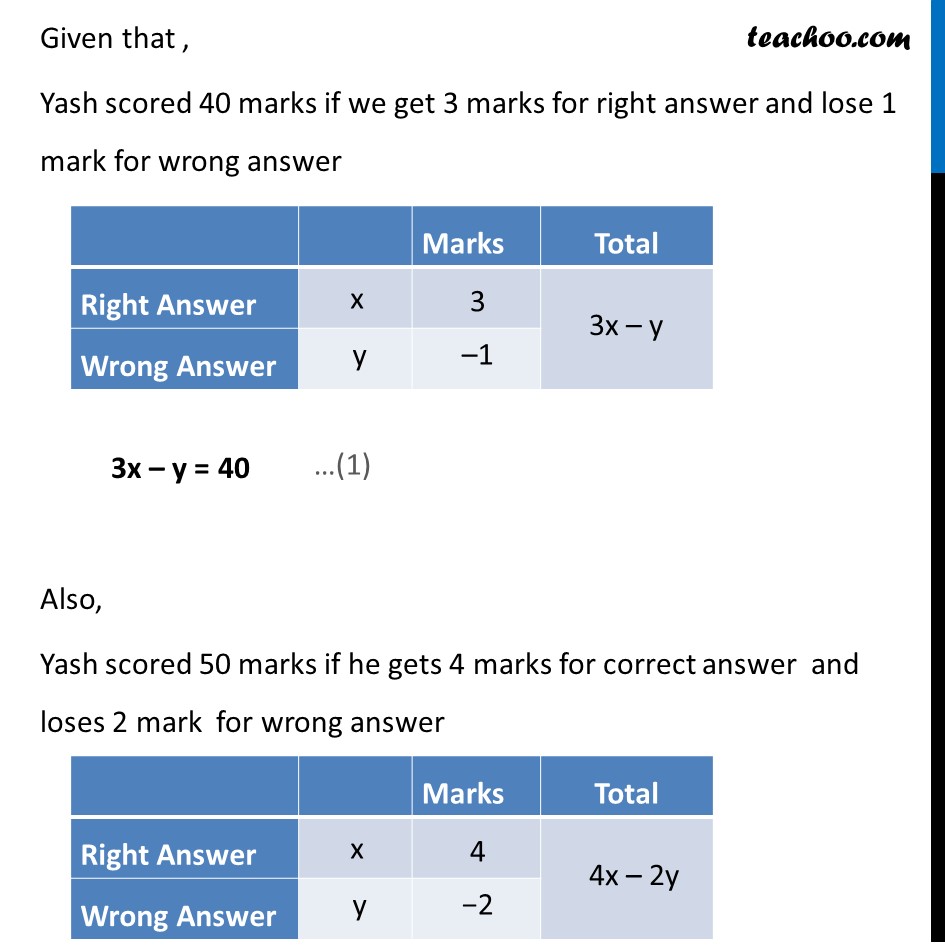
Question4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method : (iii) Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test? Let Number of Right answers be x & Number of Wrong answers be y Given that , Yash scored 40 marks if we get 3 marks for right answer and lose 1 mark for wrong answer 3x – y = 40 Also, Yash scored 50 marks if he gets 4 marks for correct answer and loses 2 mark for wrong answer 4x – 2y = 50 2(2x – y)= 50 (2x – y) = 50/2 2x – y = 25 Hence, our equations are 3x – y = 40 …(1) 2x – y = 25 …(2) From (1) 3x – y = 40 3x – 40 = y y = 3x – 40 Putting value of y in (2) 2x – y = 25 2x – (3x – 40) = 25 2x – 3x + 40 = 25 2x – 3x = 25 – 40 −x = −15 x = 15 Putting x in (1) 3x – y = 40 3(15) – y = 40 3(15) – y = 40 45 – y = 40 45 – 40 = y 5 = y y = 5 Therefore x = 15, y = 5 is the solution So, Number of right answers = x = 15 Number of wrong answers = y = 5 Total questions in the test = x + y = 15 + 5 = 20