Show that triangle of maximum area that can be inscribed in a circle

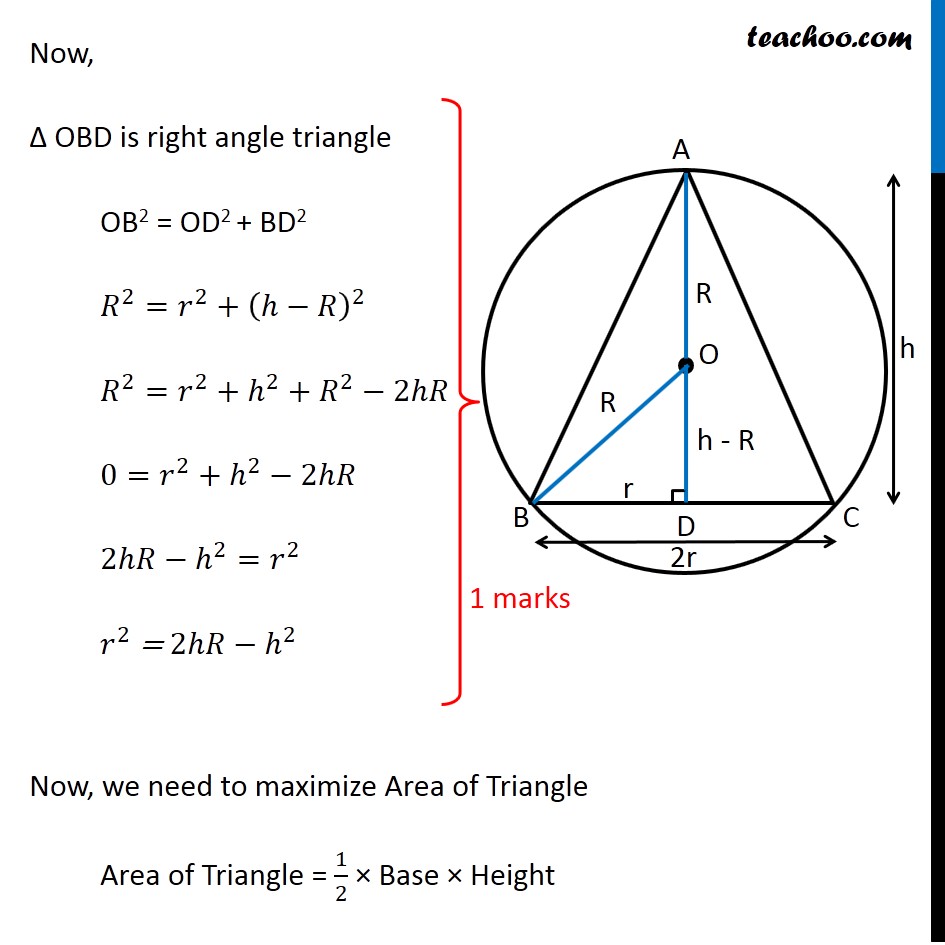
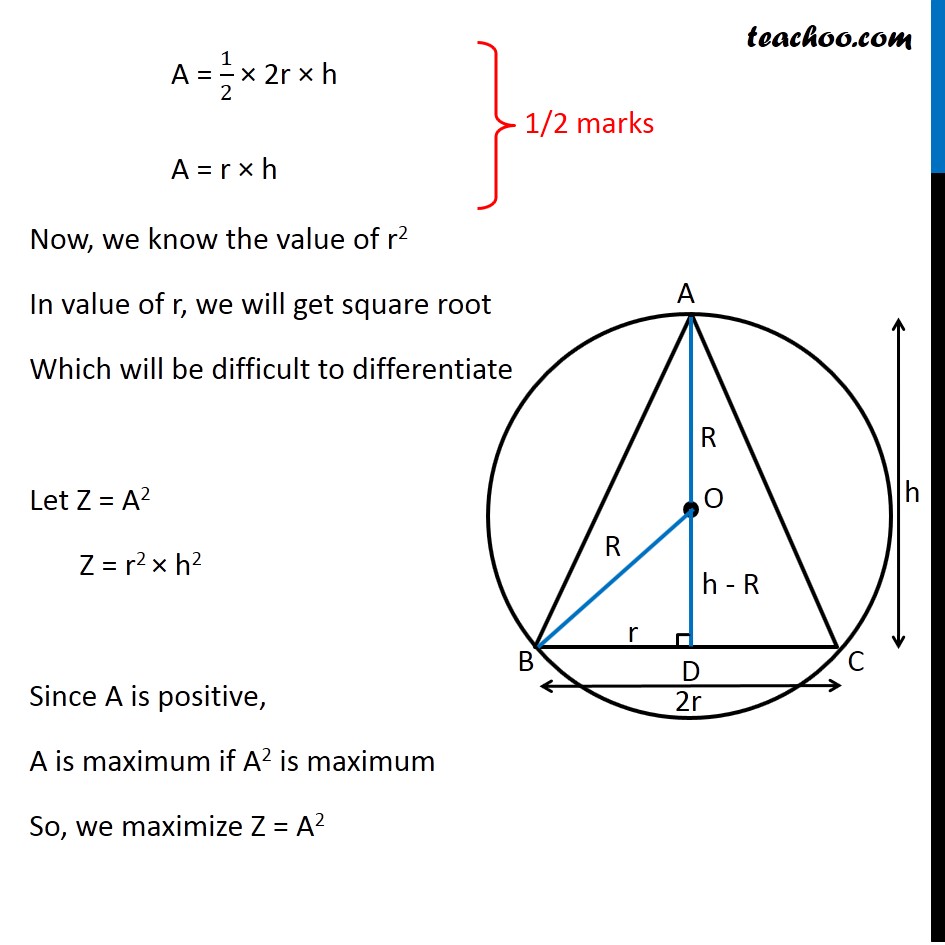
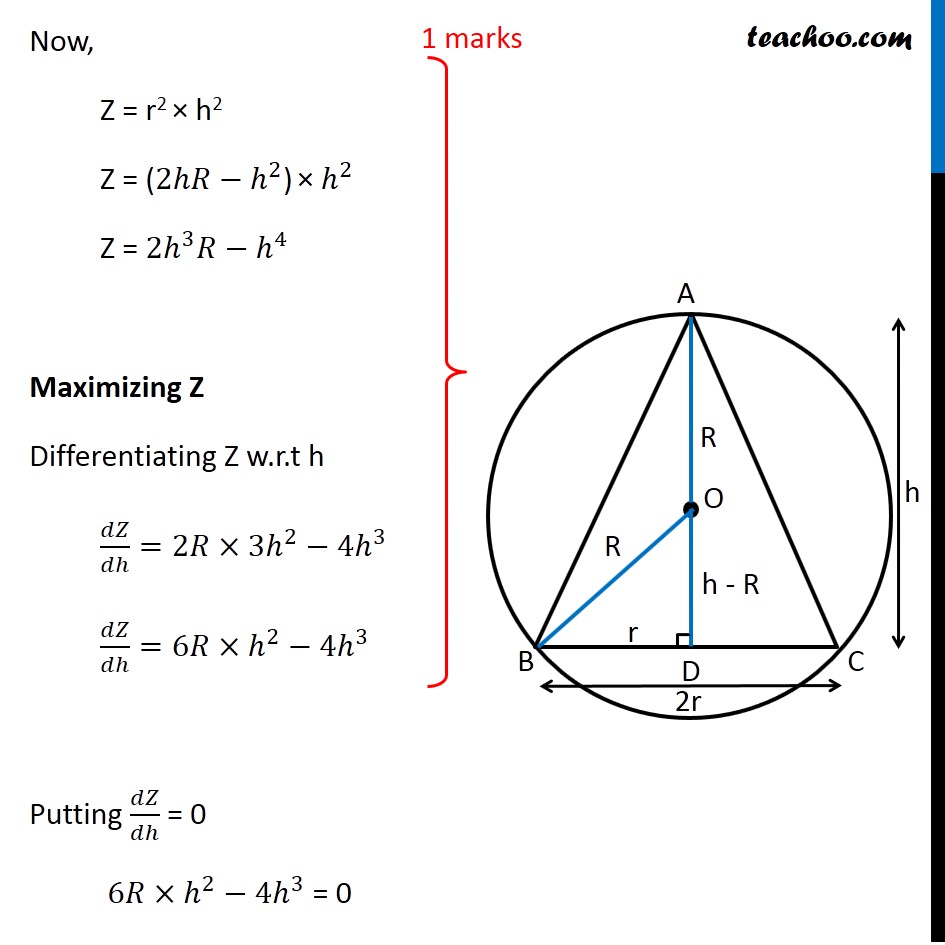
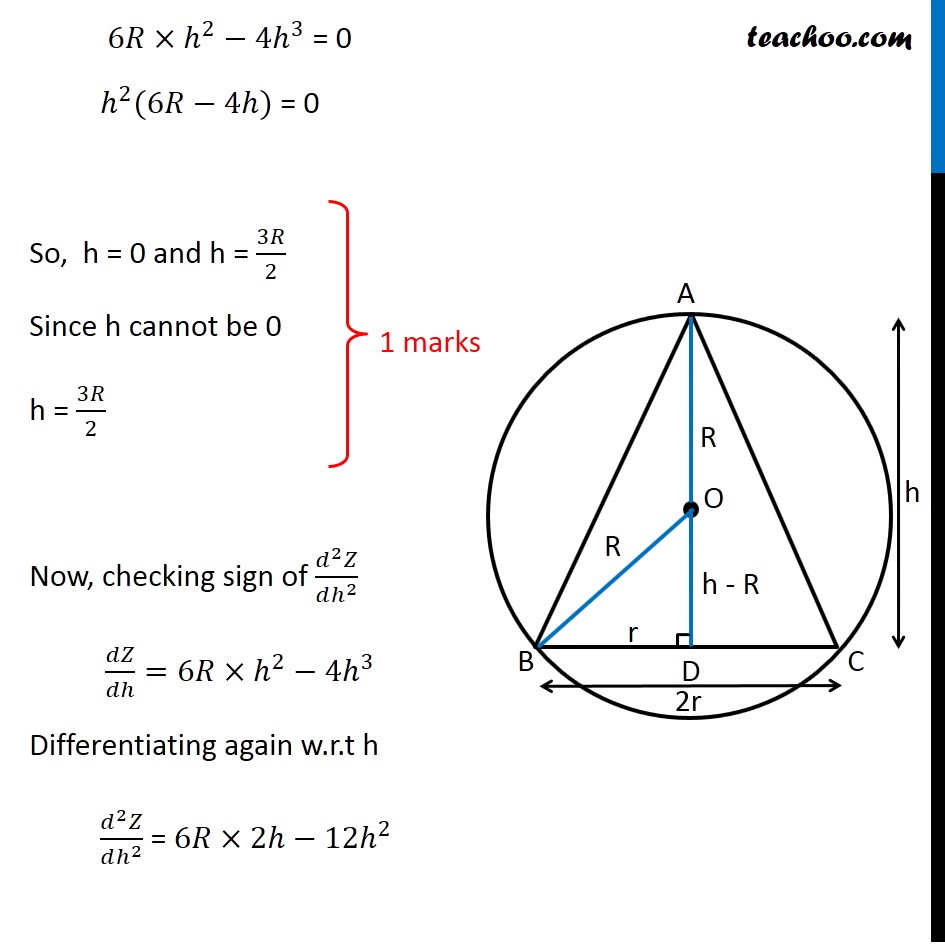
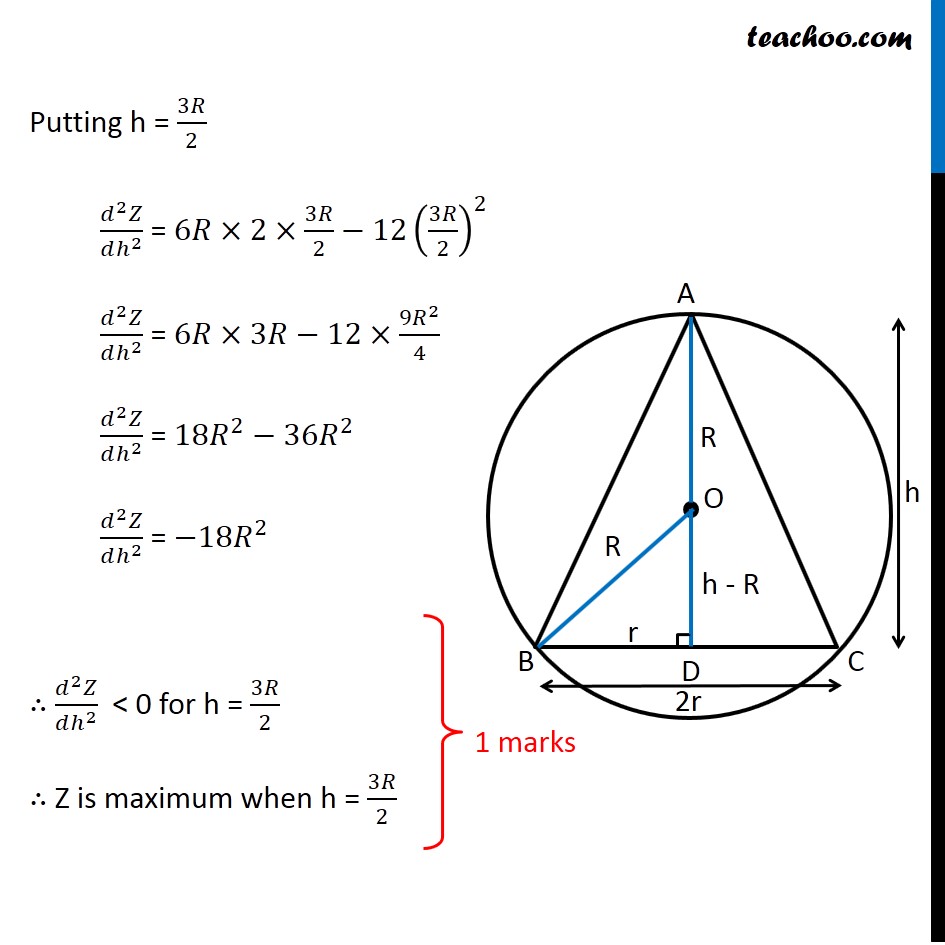
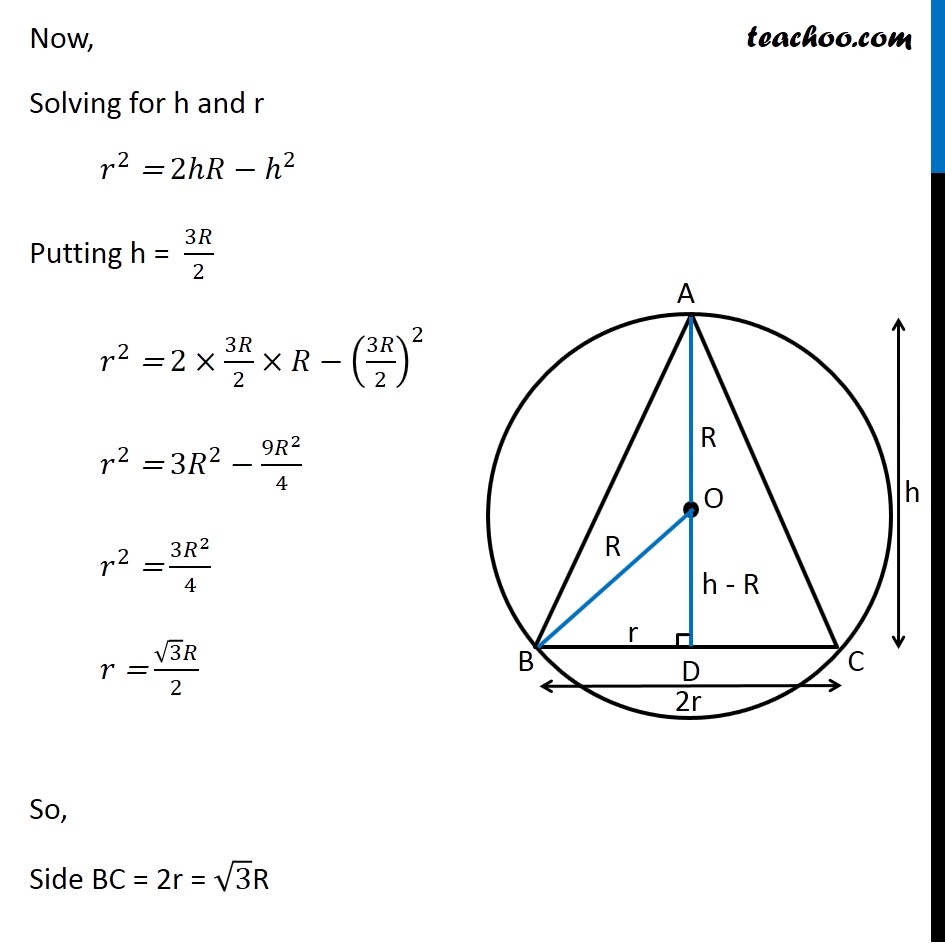
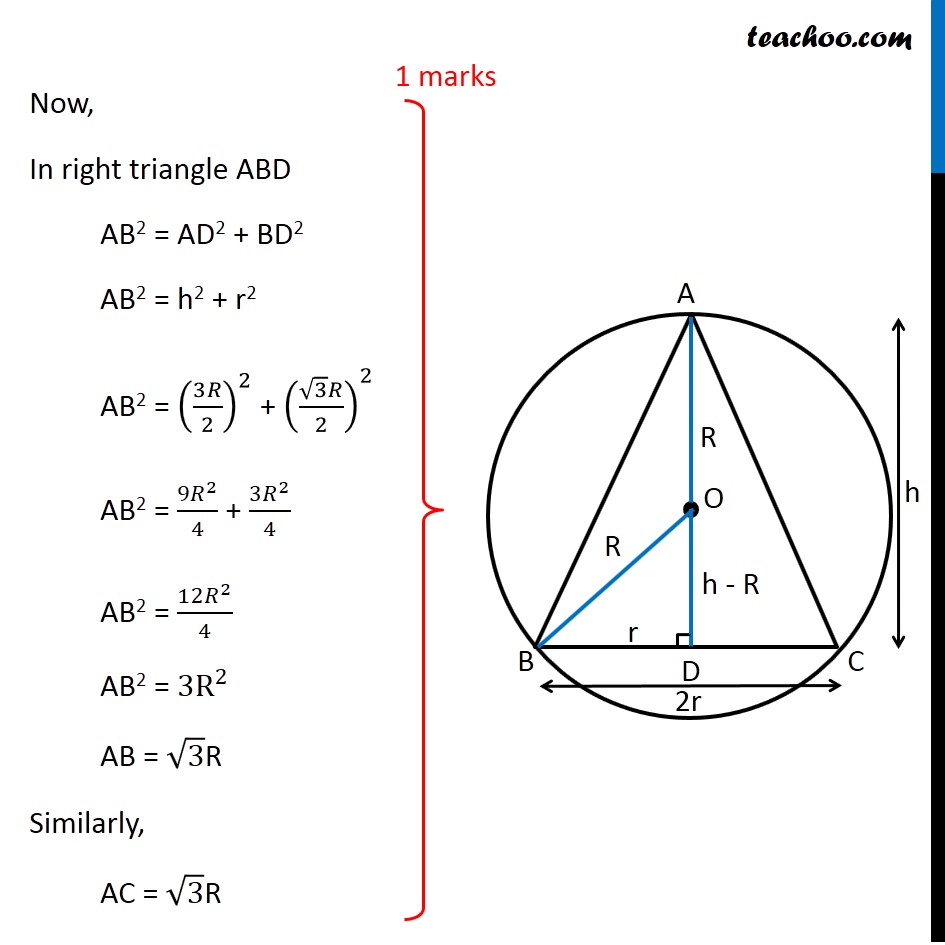
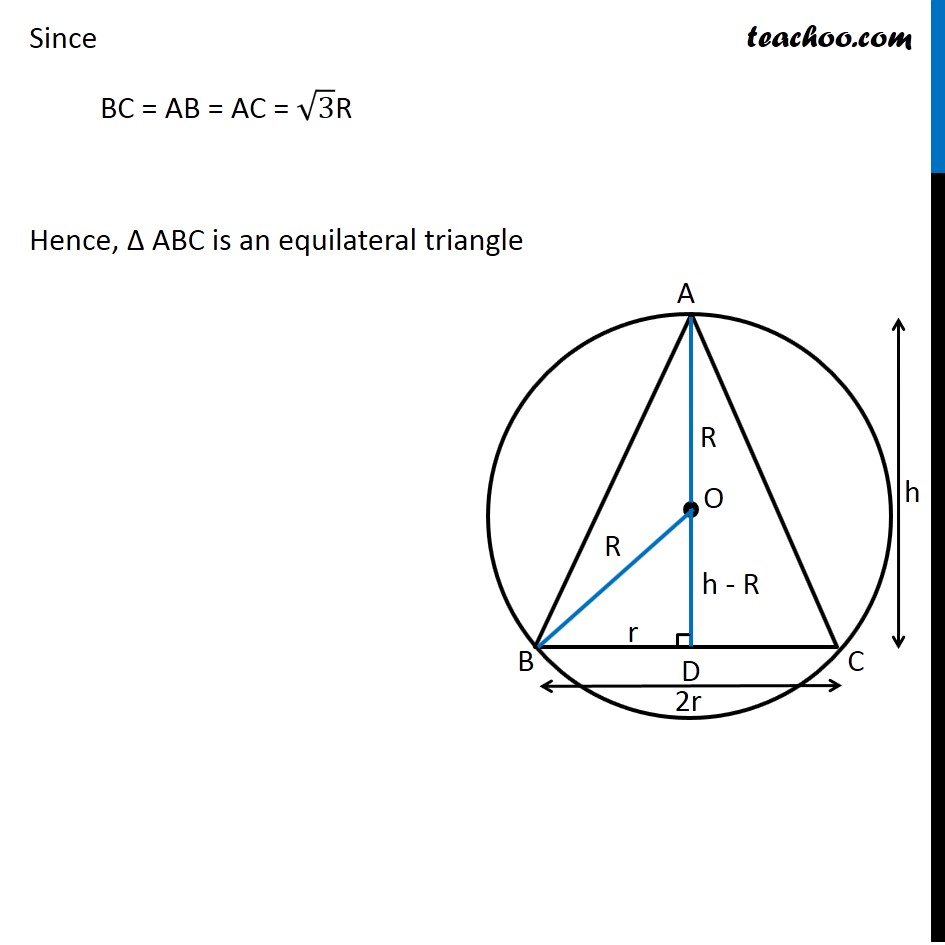
Question 35 (OR 2nd Question) Show that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle. Let R be the radius of Circle and h be height of triangle 2r be the base of triangle Let AD be the height, it is perpendicular to BC ∴ OD be perpendicular to chord BC Since perpendicular from chord bisects the chord BD = 𝐵𝐶/2 = r Now, Δ OBD is right angle triangle OB2 = OD2 + BD2 𝑅^2=𝑟^2+(ℎ−𝑅)^2 𝑅^2=𝑟^2+ℎ^2+𝑅^2−2ℎ𝑅 0=𝑟^2+ℎ^2−2ℎ𝑅 2ℎ𝑅−ℎ^2=𝑟^2 𝑟^2 = 2ℎ𝑅−ℎ^2 Now, we need to maximize Area of Triangle Area of Triangle = 1/2 × Base × Height A = 1/2 × 2r × h A = r × h Now, we know the value of r2 In value of r, we will get square root Which will be difficult to differentiate Let Z = A2 Z = r2 × h2 Since A is positive, A is maximum if A2 is maximum So, we maximize Z = A2 Now, Z = r2 × h2 Z = (2ℎ𝑅−ℎ^2) × ℎ^2 Z = 2ℎ^3 𝑅−ℎ^4 Maximizing Z Differentiating Z w.r.t h 𝑑𝑍/𝑑ℎ=2𝑅×3ℎ^2−4ℎ^3 𝑑𝑍/𝑑ℎ=6𝑅×ℎ^2−4ℎ^3 Putting 𝑑𝑍/𝑑ℎ = 0 6𝑅×ℎ^2−4ℎ^3 = 0 6𝑅×ℎ^2−4ℎ^3 = 0 ℎ^2 (6𝑅−4ℎ) = 0 So, h = 0 and h = 3𝑅/2 Since h cannot be 0 h = 3𝑅/2 Now, checking sign of (𝑑^2 𝑍)/(𝑑ℎ^2 ) " " 𝑑𝑍/𝑑ℎ=6𝑅×ℎ^2−4ℎ^3 Differentiating again w.r.t h (𝑑^2 𝑍)/(𝑑ℎ^2 ) = 6𝑅×2ℎ−12ℎ^2 Putting h = 3𝑅/2 (𝑑^2 𝑍)/(𝑑ℎ^2 ) = 6𝑅×2×3𝑅/2−12(3𝑅/2)^2 (𝑑^2 𝑍)/(𝑑ℎ^2 ) = 6𝑅×3𝑅−12×(9𝑅^2)/4 (𝑑^2 𝑍)/(𝑑ℎ^2 ) = 18𝑅^2−36𝑅^2 (𝑑^2 𝑍)/(𝑑ℎ^2 ) = −18𝑅^2 ∴ (𝑑^2 𝑍)/(𝑑ℎ^2 ) < 0 for h = 3𝑅/2 ∴ Z is maximum when h = 3𝑅/2 Now, Solving for h and r 𝑟^2 = 2ℎ𝑅−ℎ^2 Putting h = 3𝑅/2 𝑟^2 = 2×3𝑅/2×𝑅−(3𝑅/2)^2 𝑟^2 = 3𝑅^2−(9𝑅^2)/4 𝑟^2 = (3𝑅^2)/4 𝑟 = (√3 𝑅)/2 So, Side BC = 2r = √3R Now, In right triangle ABD AB2 = AD2 + BD2 AB2 = h2 + r2 AB2 = (3𝑅/2)^2 + ((√3 𝑅)/2)^2 AB2 = (9𝑅^2)/4 + (3𝑅^2)/4 AB2 = (12𝑅^2)/4 AB2 = 3R^2 AB = √3R Similarly, AC = √3R Since BC = AB = AC = √3R Hence, Δ ABC is an equilateral triangle