CBSE Class 12 Sample Paper for 2020 Boards
You are here
CBSE Class 12 Sample Paper for 2020 Boards
Last updated at August 14, 2026 by Teachoo
Transcript
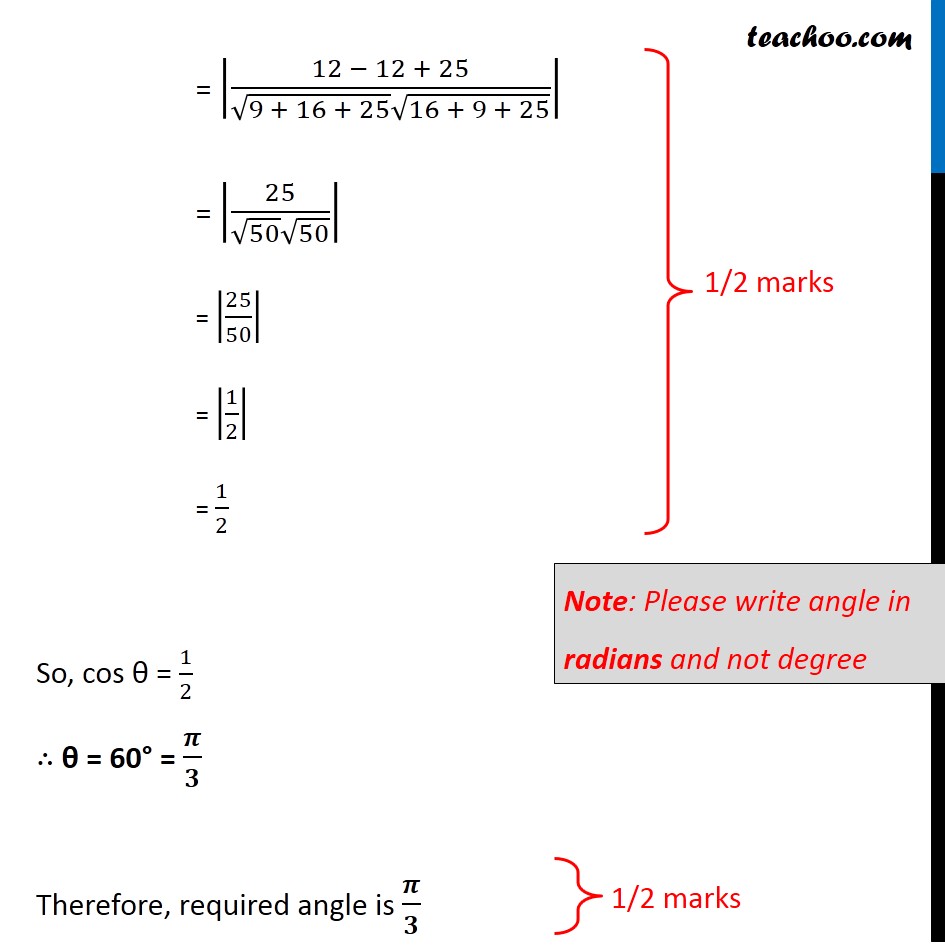
Question 25 Find the acute angle between the lines (𝑥 − 4)/3 = (𝑦 + 3)/4 = (𝑧 + 1)/5 and (𝑥 − 1)/4 = (𝑦 + 1)/(−3) = (𝑧 + 10)/5 Angle between the pair of lines (𝑥 − 𝑥_1)/𝑎_1 = (𝑦 − 𝑦_1)/𝑏_1 = (𝑧 − 𝑧_1)/𝑐_1 and (𝑥 − 𝑥_2)/𝑎_2 = (𝑦 − 𝑦_2)/𝑏_2 = (𝑧 − 𝑧_2)/𝑐_2 is given by cos θ = |(𝑎_1 𝑎_2 + 𝑏_1 𝑏_2 + 𝑐_1 𝑐_2)/(√(〖𝑎_1〗^2 + 〖𝑏_1〗^2 + 〖𝑐_1〗^2 ) √(〖𝑎_2〗^2 + 〖𝑏_2〗^2 + 〖𝑐_2〗^2 ))| (𝒙 − 𝟒)/𝟑 = (𝒚 + 𝟑)/𝟒 = (𝒛 + 𝟏)/𝟓 Comparing with (𝑥 − 𝑥_1)/𝑎_1 = (𝑦 − 𝑦_1)/𝑏_1 = (𝑧 − 𝑧_1)/𝑐_1 𝑎1 = 3, b1 = 4, c1 = 4 (𝒙 − 𝟏)/𝟒 = (𝒚 + 𝟏)/(−𝟑) = (𝒛 + 𝟏𝟎)/𝟓 Comparing with (𝑥 − 𝑥_2)/𝑎_2 = (𝑦 − 𝑦_2)/𝑏_2 = (𝑧 − 𝑧_2)/𝑐_2 𝑎2 = 4, 𝑏2 = –3, 𝑐2 = 5 Now, cos θ = |(𝑎_1 𝑎_2 + 𝑏_1 𝑏_2 + 𝑐_1 𝑐_2)/(√(〖𝑎_1〗^2 + 〖𝑏_1〗^2 + 〖𝑐_1〗^2 ) √(〖𝑎_2〗^2 + 〖𝑏_2〗^2 + 〖𝑐_2〗^2 ))| = |(3 × 4 + 4 × (−3) + 5 × 5)/(√(3^2 + 4^2 + 5^2 ) √(4^2 +(−3)^2 + 5^2 ))| = |(12 − 12 + 25)/(√(9 + 16 + 25) √(16 + 9 + 25))| = |25/(√50 √50)| = |25/50| = |1/2| = 1/2 So, cos θ = 1/2 ∴ θ = 60° = 𝝅/𝟑 Therefore, required angle is 𝝅/𝟑 Note: Please write angle in radians and not degree
