sin (2π + x) = sin x
cos (2π + x) = cos x
tan (2π + x) = tan x
Here x is an acute angle.
and 2π = 2 × 180° = 360°
Let’s see why there are same.
Suppose x = 390°
x = 360° + 30°
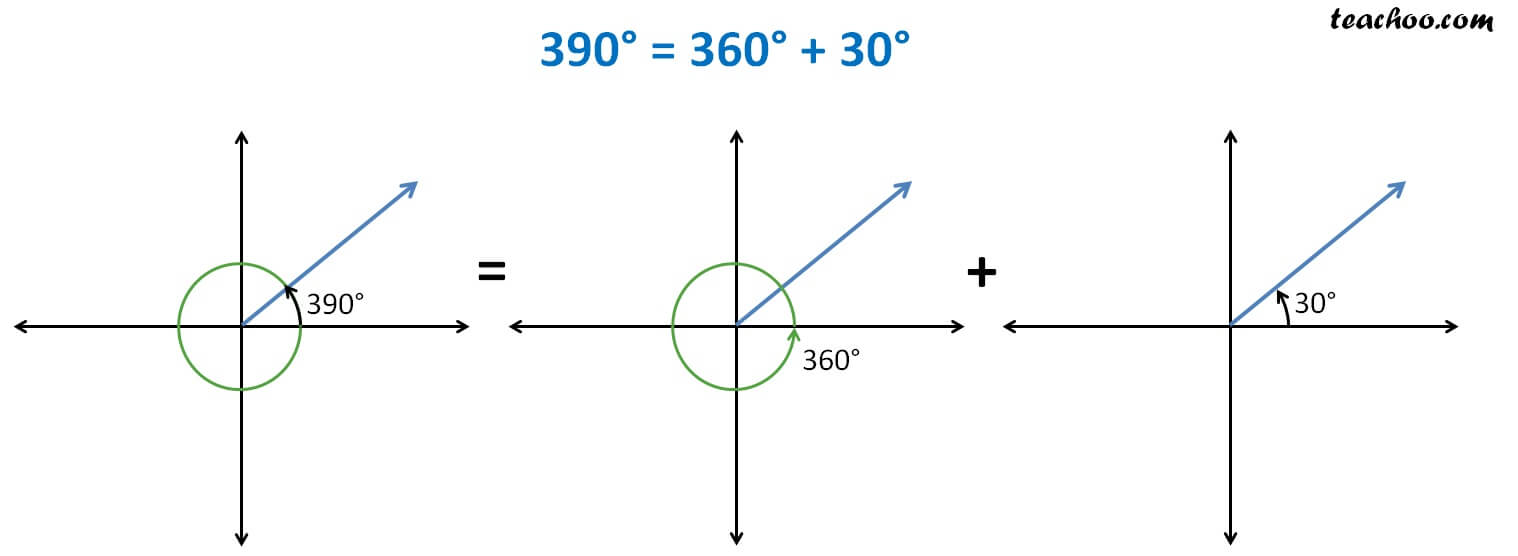
We note that
x = 390° is the same as 30°
So, we can write
cos (390°) = cos (30°)
sin (390°) = sin (30°)
tan (390°) = tan (30°)
Similarly,
if the angle was
x = 750°
x = 2 × 360° + 30°
Thus, we rotate twice and come back to 30°
∴ x = 750° is the same as 30°
So, we can write
cos (750°) = cos (30°)
sin (750°) = sin (30°)
tan (750°) = tan (30°)
Thus, we observe that
sin (n × 360° + x) = sin x
where n = 1, 2, 3, 4, ….
Writing in radians
sin (n × 2π + x) = sin x
cos (n × 2π + x) = cos x
tan (n × 2π + x) = tan x
where n = 1, 2, 3, 4, ….
Note: For sec, cosec, cot … we convert them into sin, cos, tan and apply the sin, cos, tan formula
Let’s try some questions
Find cos 390°
First, we convert 390° into radians.
We multiply by π/180
x = 390 × π/180
x = π × 390/180
x = π × 13/6
x = 13π/6
So, cos 390° = cos 13π/6
.jpg)
Thus,
cos 13π/6
= cos (2π + π/6)
Since values of cos x repeats after an interval of 2π ,hence ignoring 2π
= cos (π/6)
= cos (180/6°)
= cos 30°
= √3/2
Find value of tan (–15 π /4)
tan (–15π/4)
As tan (–x) = – tan x
= – tan (15π/4)
.jpg)
= – tan (4π – π/4)
= – tan (–π/4)
As tan (–x) = – tan x
= – (– tan (π/4))
= tan (π/4)
= tan (180/4 °)
= tan (45°)
= 1
∴ tan (–15π/4) = 1
