Theorem 9.7 - Chapter 9 Class 9 Circles

Transcript

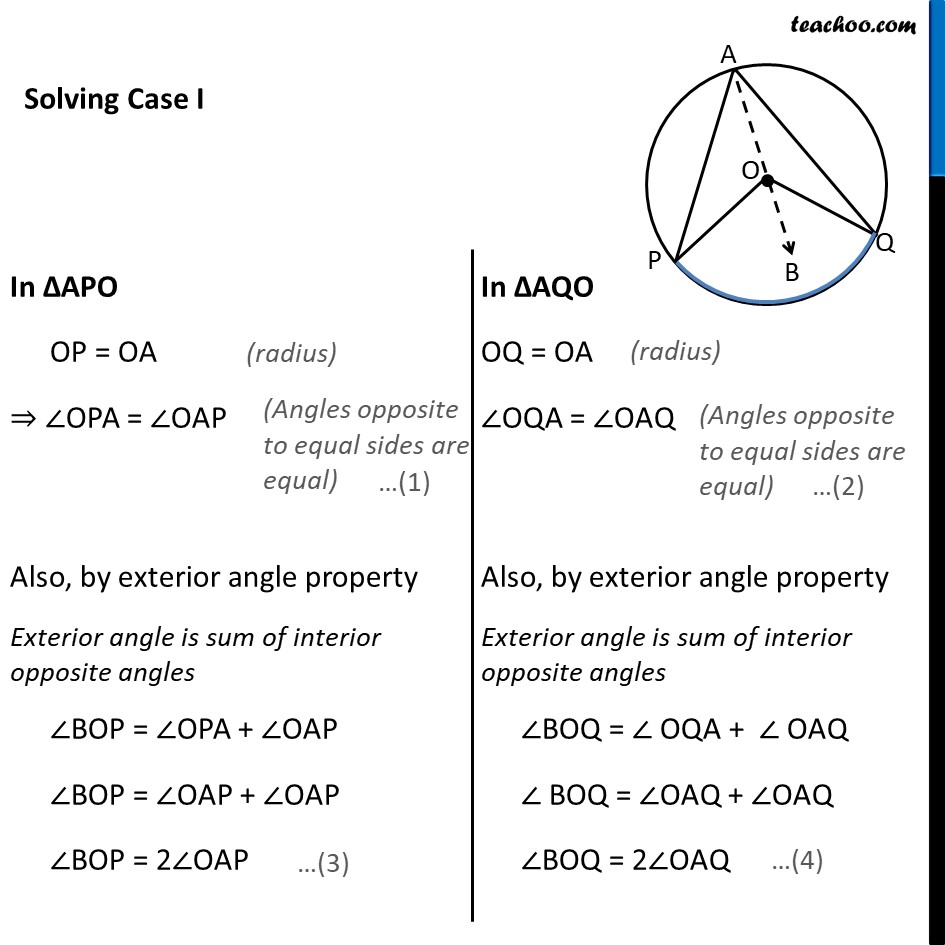
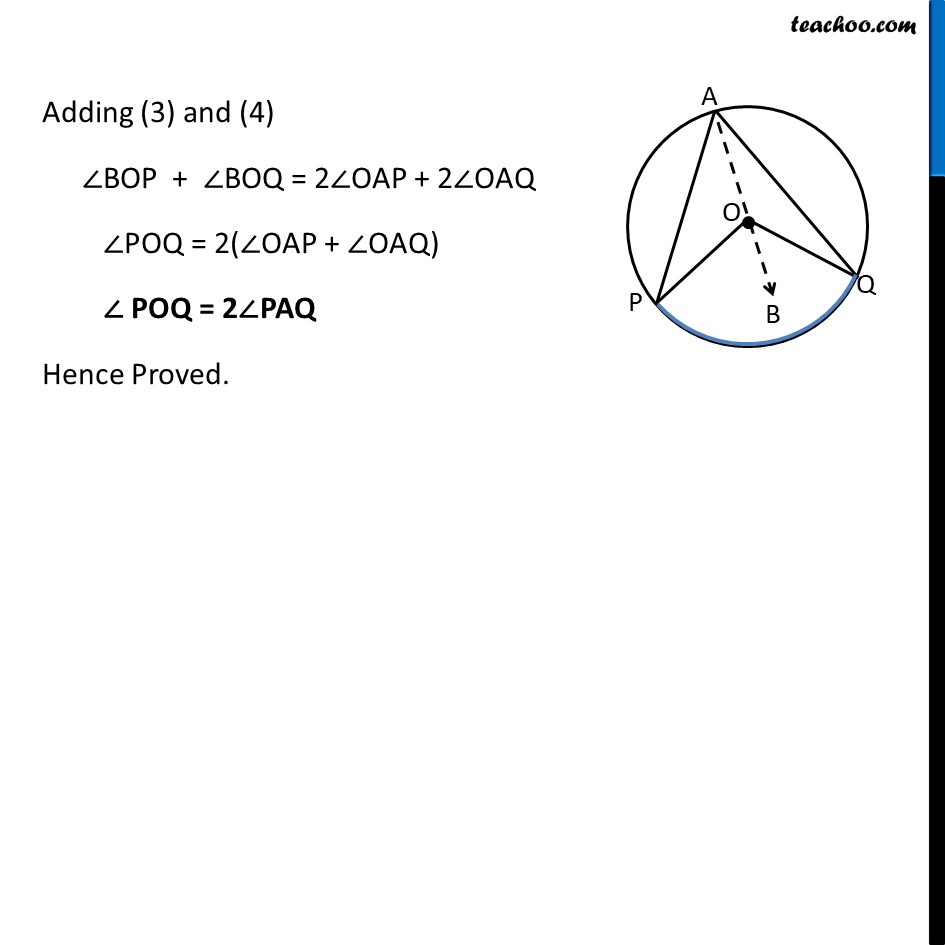
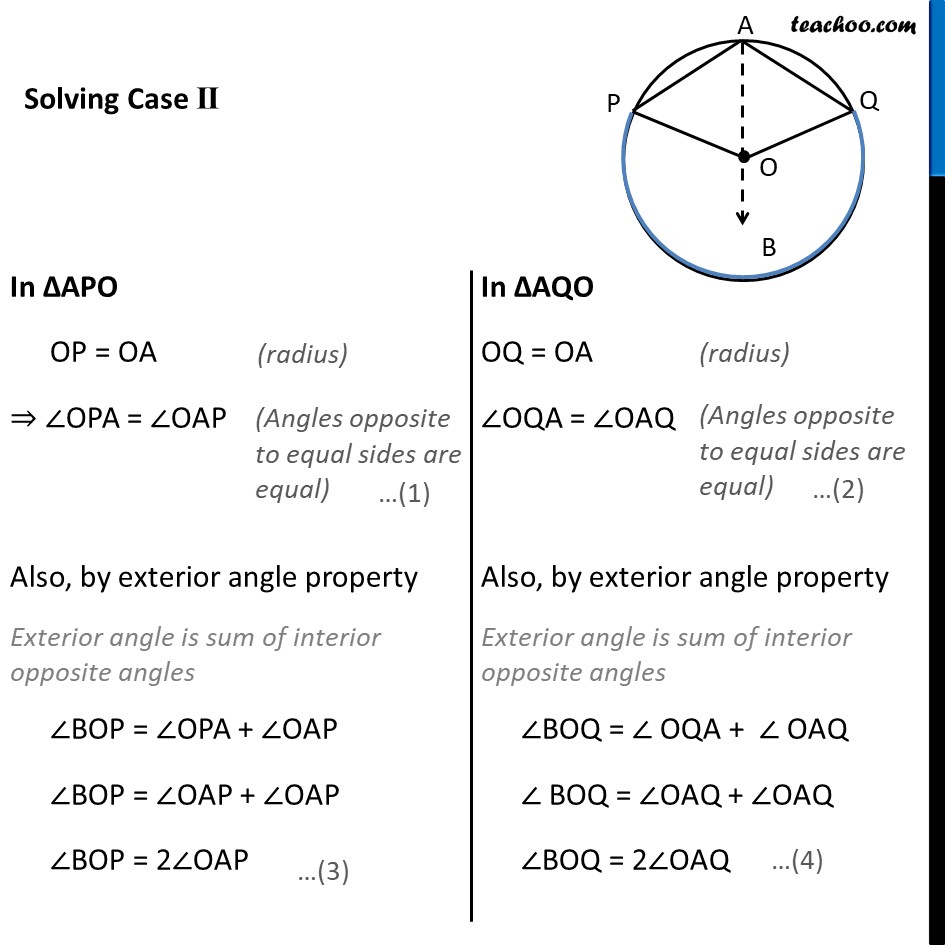
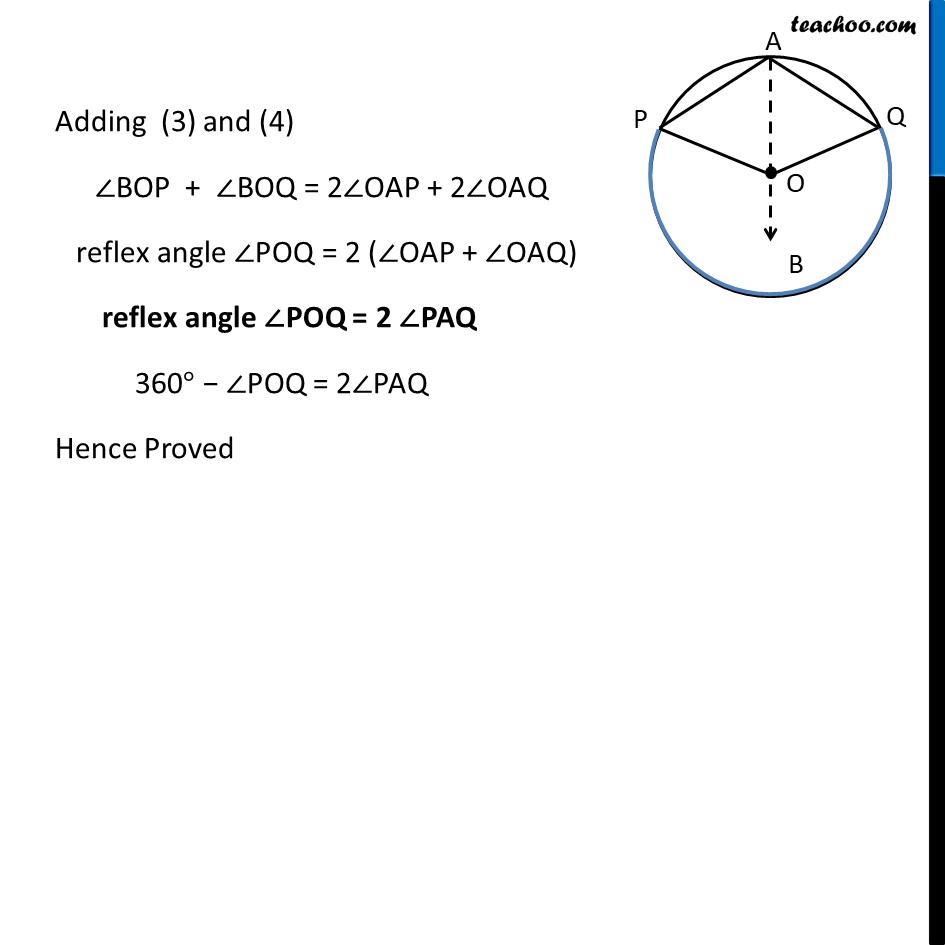
Theorem 9.8 The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. Given : A circle with center at O. Arc PQ of this circle subtends angles POQ at centre O & ∠ PAQ at a point A remaining part of circle. To Prove : ∠POQ = 2∠PAQ Construction : Join AO and extend it to point B Proof : There are two general cases Theorem 9.8 The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. Given : A circle with center at O. Arc PQ of this circle subtends angles POQ at centre O & ∠ PAQ at a point A remaining part of circle. To Prove : ∠POQ = 2∠PAQ Construction : Join AO and extend it to point B Proof : There are two general cases In ∆APO OP = OA ⇒ ∠OPA = ∠OAP Also, by exterior angle property Exterior angle is sum of interior opposite angles ∠BOP = ∠OPA + ∠OAP ∠BOP = ∠OAP + ∠OAP ∠BOP = 2∠OAP In ∆AQO OQ = OA ∠OQA = ∠OAQ Also, by exterior angle property Exterior angle is sum of interior opposite angles ∠BOQ = ∠ OQA + ∠ OAQ ∠ BOQ = ∠OAQ + ∠OAQ ∠BOQ = 2∠OAQ Adding (3) and (4) ∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ ∠POQ = 2(∠OAP + ∠OAQ) ∠ POQ = 2∠PAQ Hence Proved. Solving Case II In ∆APO OP = OA ⇒ ∠OPA = ∠OAP Also, by exterior angle property Exterior angle is sum of interior opposite angles ∠BOP = ∠OPA + ∠OAP ∠BOP = ∠OAP + ∠OAP ∠BOP = 2∠OAP In ∆AQO OQ = OA ∠OQA = ∠OAQ Also, by exterior angle property Exterior angle is sum of interior opposite angles ∠BOQ = ∠ OQA + ∠ OAQ ∠ BOQ = ∠OAQ + ∠OAQ ∠BOQ = 2∠OAQ Adding (3) and (4) ∠BOP + ∠BOQ = 2∠OAP + 2∠OAQ reflex angle ∠POQ = 2 (∠OAP + ∠OAQ) reflex angle ∠POQ = 2 ∠PAQ 360° − ∠POQ = 2∠PAQ Hence Proved Theorem : Angle subtended by a diameter/semicircle on any point of circle is 90° Given : A circle with centre at O. PQ is the diameter of circle subtending ∠PAQ at point A on circle. To Prove : ∠PAQ = 90° Proof : Now, POQ is a straight line passing through center O. ∴ Angle subtended by arc PQ at O is ∠POQ = 180° Also, By theorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. Thus, ∠ POQ = 2∠PAQ "∠ POQ" /2 = ∠PAQ (180° )/2 = ∠PAQ 90° = ∠PAQ ∠PAQ = 90° Hence, Proved.