Theorem 10.4 - Chapter 10 Class 9 Circles (Term 2)
Last updated at Aug. 13, 2018 by Teachoo
Theorems
Theorem 10.1
Theorem 10.2 Important
Theorem 10.3 Important Deleted for CBSE Board 2023 Exams
Theorem 10.4 You are here
Theorem 10.5
Theorem 10.6 Important
Theorem 10.7
Theorem 10.8 Important
Theorem 10.9
Theorem 10.10 Important
Theorem 10.11
Theorem 10.12 Important
Angle in a semicircle is a right angle Important
Chapter 10 Class 9 Circles
Serial order wise
Transcript
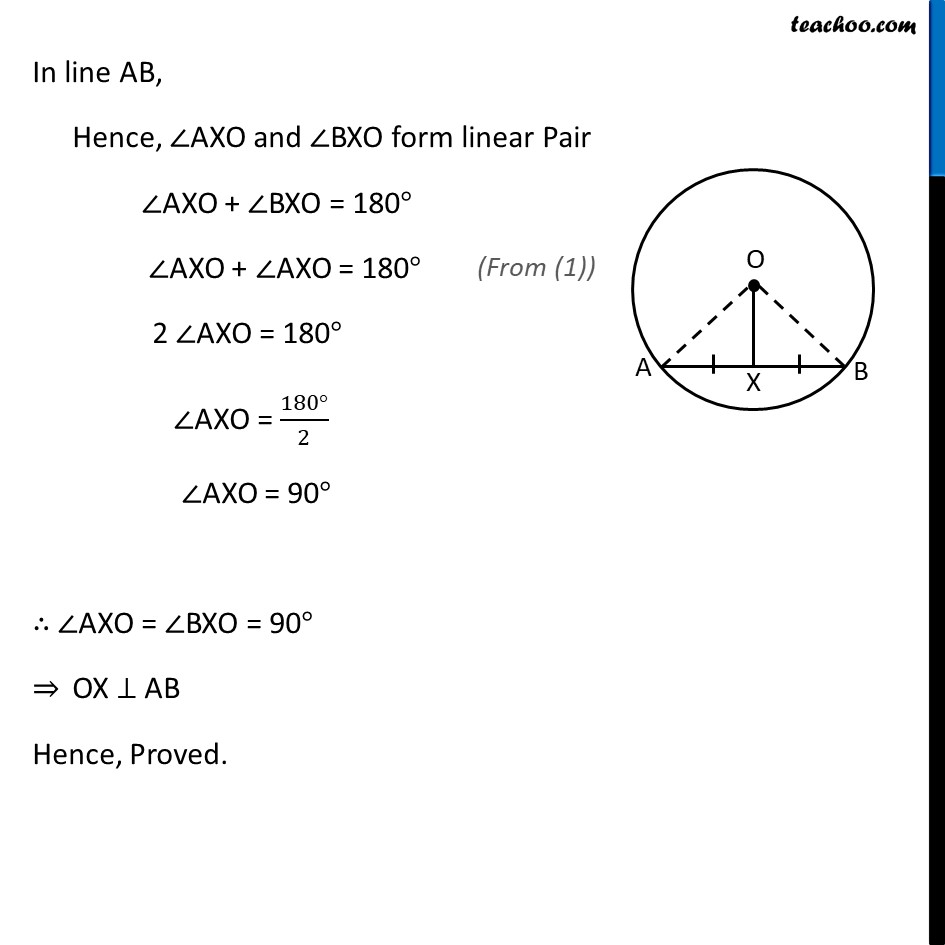
Theorem 10.4 The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord. Given : A circle with center at O. AB is chord of circle & OX bisects AB i.e. AX = BX To Prove : OX ⊥ AB Proof : In ∆AOX & ∆BOX OA = OB OX = OX AX = BX ∴ ∆AOX ≅ ∆BOX ∠ AXO = BXO In line AB, Hence, ∠AXO and ∠BXO form linear Pair ∠AXO + ∠BXO = 180° ∠AXO + ∠AXO = 180° 2 ∠AXO = 180° ∠AXO = (180°)/2 ∠AXO = 90° ∴ ∠AXO = ∠BXO = 90° ⇒ OX ⊥ AB Hence, Proved.
