Misc 14 - Chapter 6 Class 12 Application of Derivatives (Important Question)

Transcript

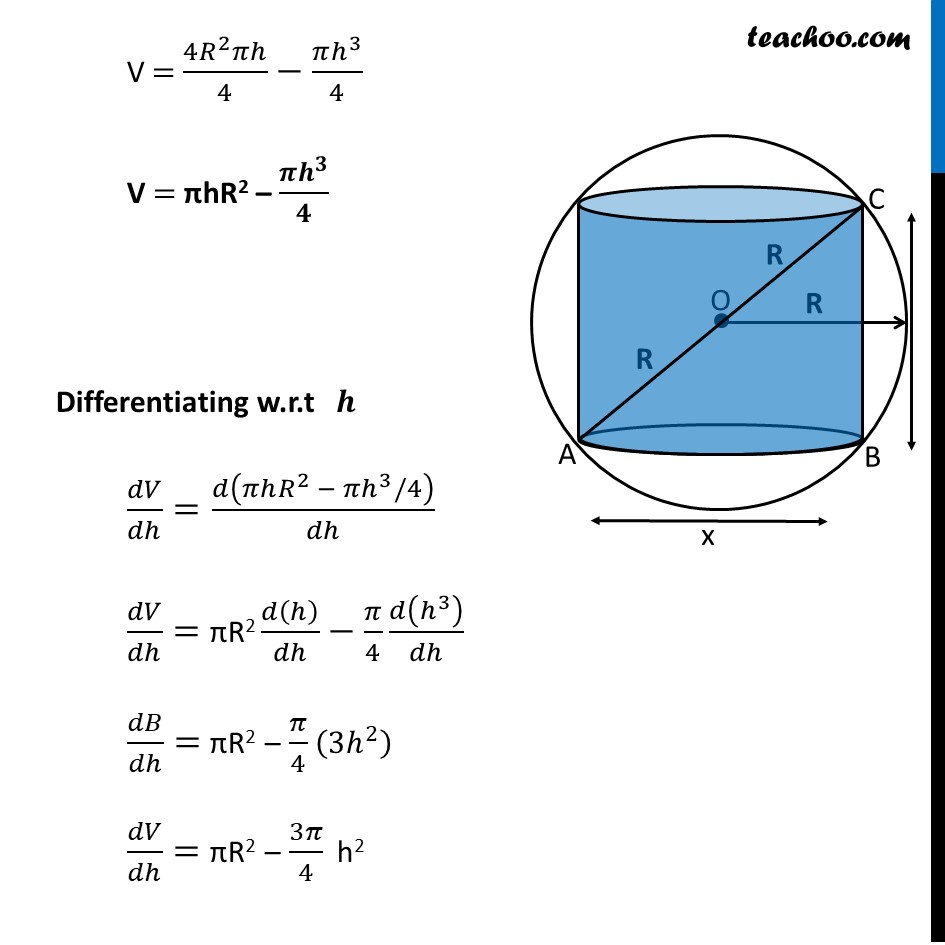
Misc 14 Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2𝑅/√3 . Also find the maximum volume.Given Radius of sphere = R Let h be the height & 𝒙 be the diameter of cylinder In ∆ 𝑨𝑩𝑪 Using Pythagoras theorem (𝐶𝐵)^2+(𝐴𝐵)^2=(𝐴𝐶)^2 h2 + 𝑥^2=(𝑅+𝑅)^2 h2 + 𝑥2 =(2𝑅)^2 h2 + 𝑥2 = 4R2 𝒙2 = 4R2 – h2 We need to find maximum volume of cylinder Let V be the volume of cylinder V = π (𝑟𝑎𝑑𝑖𝑢𝑠)^2×(ℎ𝑒𝑖𝑔ℎ𝑡) V = π (𝑥/2)^2× ℎ V = π × 𝑥^2/4× ℎ V = π ((4𝑅^2 − ℎ^2 ))/4 × ℎ V = (4𝑅^2 𝜋ℎ)/4−(𝜋ℎ^3)/4 V = πhR2 – (𝝅𝒉^𝟑)/𝟒 Differentiating w.r.t 𝒉 𝑑𝑉/𝑑ℎ=𝑑(𝜋ℎ𝑅^2 − 𝜋ℎ^3/4)/𝑑ℎ 𝑑𝑉/𝑑ℎ= πR2 𝑑(ℎ)/𝑑ℎ−𝜋/4 𝑑(ℎ^3 )/𝑑ℎ 𝑑𝐵/𝑑ℎ= πR2 – 𝜋/4 (3ℎ^2 ) 𝑑𝑉/𝑑ℎ= πR2 – 3𝜋/4 h2 Putting 𝒅𝑽/𝒅𝒉=𝟎 π R2 – 3/4 𝜋 ℎ^2=0 3/4 𝜋ℎ^2=𝜋𝑅^2 h2 = (𝜋𝑅^2)/(3/4 𝜋) h2 = (4𝑅^2)/3 h =√((4𝑅^2)/3) h = 𝟐𝑹/√𝟑 Finding (𝒅^𝟐 𝑽)/(𝒅𝒉^𝟐 ) 𝑑𝑉/𝑑ℎ=𝜋𝑅^2−3/(4 ) 𝜋 ℎ^2 Differentiating w.r.t. h (𝑑^2 𝑉)/(𝑑ℎ^2 )= 𝑑(𝜋𝑅^2 − 3/4 𝜋ℎ^2 )/𝑑ℎ (𝑑^2 𝑉)/(𝑑ℎ^2 )= 0 – 3𝜋/4 ×2ℎ (𝒅^𝟐 𝑽)/(𝒅𝒉^𝟐 )=(−𝟑𝝅𝒉)/𝟐 Since (𝒅^𝟐 𝑽)/(𝒅𝒉^𝟐 )<𝟎 for h = 2𝑅/√3 ∴ Volume is maximum for h = 2𝑅/√3 We also need to find Maximum Volume V = πhR2 – (𝜋ℎ^3)/4 V = πR2 × 2𝑅/√3 – 𝜋/4 × (2𝑅/√3)^3 V = (2𝜋𝑅^3)/√3 – 𝜋/4 ×(8𝑅^3)/(3√3) V = (2𝜋𝑅^3)/√3 – (2𝜋𝑅^3)/(3√3) V = (2𝜋𝑅^3)/√3 (1−1/3) V = (2𝜋𝑅^3)/√3 ×2/3 V = (𝟒𝝅𝑹^𝟑)/(𝟑√𝟑) cubic unit