Example 33 - Chapter 6 Class 12 Application of Derivatives (Important Question)

Transcript

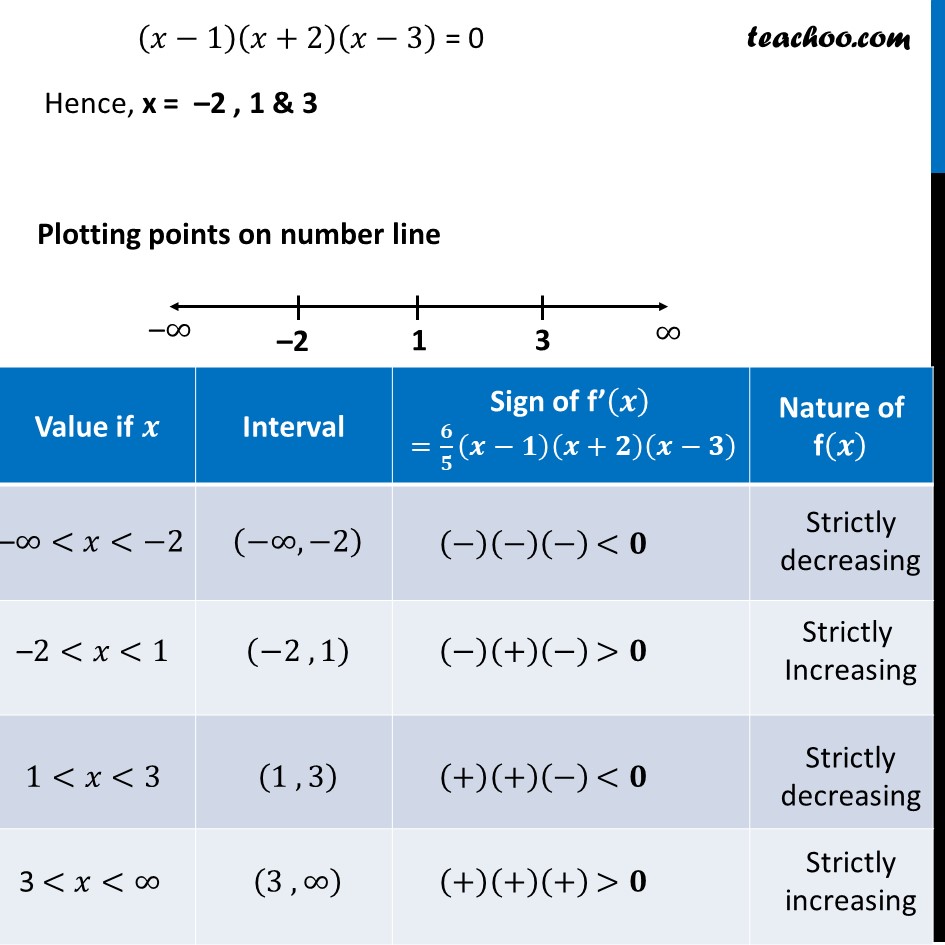
Example 33 Find intervals in which the function given by f(𝑥) =3/10 𝑥4 – 4/5 𝑥^3– 3𝑥2 + 36/5 𝑥 + 11 is (a) strictly increasing (b) strictly decreasingf(𝑥) = 3/10 𝑥4 – 4/5 𝑥^3– 3𝑥2 + 36/5 𝑥 + 11 Finding f’(𝒙) f’(𝑥) = 3/10 × 4𝑥^3 – 4/5 × 3𝑥^2 – 3 × 2x + 36/5 + 0 f’(𝑥) = 12/10 𝑥^3– 12/5 𝑥^2– 6x + 36/5 f’(𝑥) = 6/5 𝑥^3− 12/5 𝑥^2– 6x + 36/5 f’(𝑥) = 6(𝑥^3/5−(2𝑥^2)/5−𝑥+6/5) f’(𝑥) = 6((𝑥^3 − 2𝑥^2− 5𝑥 + 6)/5) = 6/5 (𝑥^3−2𝑥^2−5𝑥+6) = 6/5 (𝑥−1)(𝑥2−𝑥−6) = 6/5 (𝑥−1)(𝑥2−3𝑥+2𝑥−6) = 6/5 (𝑥−1)[𝑥(𝑥−3)+2(𝑥−3)] = 6/5 (𝑥−1)(𝑥+2)(𝑥−3) Hence, f’(𝒙) = 𝟔/𝟓 (𝒙−𝟏)(𝒙+𝟐)(𝒙−𝟑) Putting f’(𝒙) = 0 𝟔/𝟓 (𝒙−𝟏)(𝒙+𝟐)(𝒙−𝟑) = 0 f’(𝑥) = 6((𝑥^3 − 2𝑥^2− 5𝑥 + 6)/5) = 6/5 (𝑥^3−2𝑥^2−5𝑥+6) = 6/5 (𝑥−1)(𝑥2−𝑥−6) = 6/5 (𝑥−1)(𝑥2−3𝑥+2𝑥−6) = 6/5 (𝑥−1)[𝑥(𝑥−3)+2(𝑥−3)] = 6/5 (𝑥−1)(𝑥+2)(𝑥−3) Hence, f’(𝒙) = 𝟔/𝟓 (𝒙−𝟏)(𝒙+𝟐)(𝒙−𝟑) Putting f’(𝒙) = 0 𝟔/𝟓 (𝒙−𝟏)(𝒙+𝟐)(𝒙−𝟑) = 0 (𝑥−1)(𝑥+2)(𝑥−3) = 0 Hence, x = –2 , 1 & 3 Plotting points on number line Hence, f(𝑥) is strictly decreasing on the interval 𝑥 ∈ (−∞,−𝟐)& (𝟏 , 𝟑) f(𝑥) is strictly increasing on the interval 𝑥 ∈ (−𝟐,𝟏) & (𝟑 , ∞)