Theorem 6.8 - Chapter 6 Class 10 Triangles

Transcript

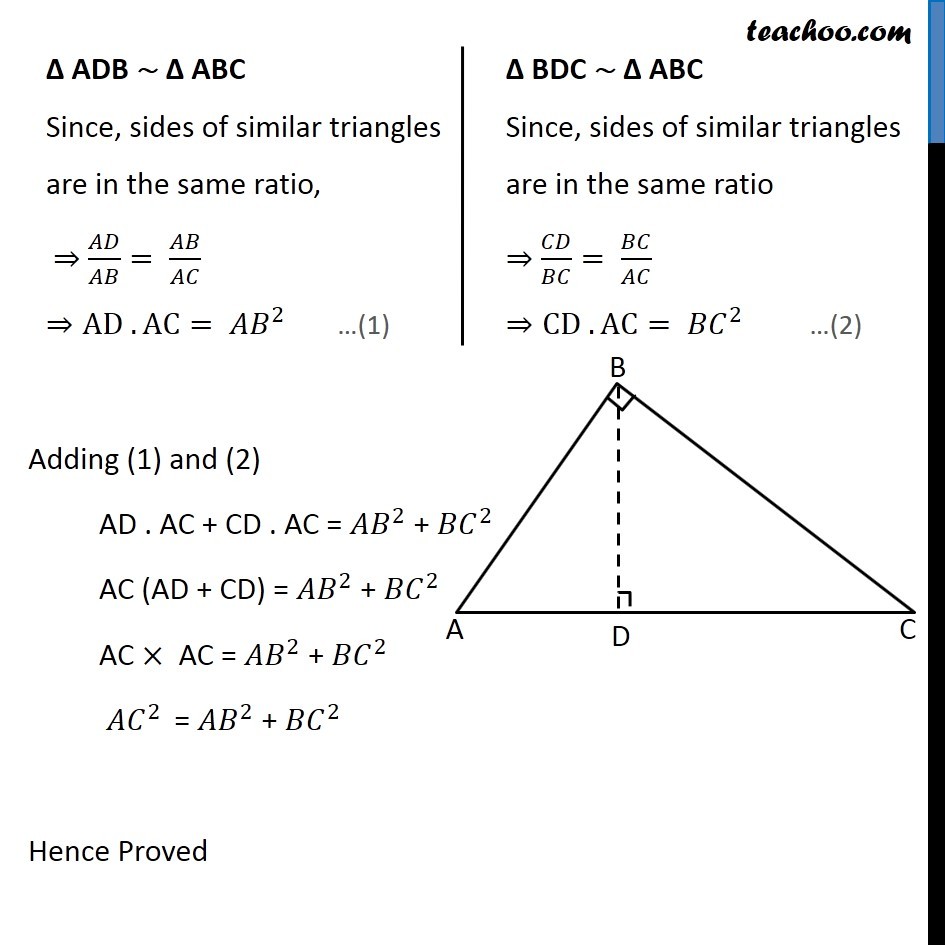
Theorem 6.8 (Pythagoras Theorem) : If a right triangle, the square of the hypotenuse is equal to the sum of the squares of other two sides. Given: ∆ABC right angle at B To Prove: 〖𝐴𝐶〗^2= 〖𝐴𝐵〗^2+〖𝐵𝐶〗^2 Construction: Draw BD ⊥ AC Proof: Since BD ⊥ AC Using Theorem 6.7: If a perpendicular is drawn from the vertex of the right angle of the a right triangle to the hypotenuse then triangle on both side of the perpendicular are similar to whole triangle and to each other. Δ ADB ∼ Δ ABC Since, sides of similar triangles are in the same ratio, ⇒ 𝐴𝐷/𝐴𝐵= 𝐴𝐵/𝐴𝐶 ⇒AD . AC= 〖𝐴𝐵〗^2 Δ BDC ∼ Δ ABC Since, sides of similar triangles are in the same ratio ⇒ 𝐶𝐷/𝐵𝐶= 𝐵𝐶/𝐴𝐶 ⇒CD . AC= 〖𝐵𝐶〗^2 Adding (1) and (2) AD . AC + CD . AC = 〖𝐴𝐵〗^2 + 〖𝐵𝐶〗^2 AC (AD + CD) = 〖𝐴𝐵〗^2 + 〖𝐵𝐶〗^2 AC × AC = 〖𝐴𝐵〗^2 + 〖𝐵𝐶〗^2 〖𝐴𝐶〗^2 = 〖𝐴𝐵〗^2 + 〖𝐵𝐶〗^2 Hence Proved