Theorem 6.4 - Chapter 6 Class 10 Triangles (Term 1)

Transcript

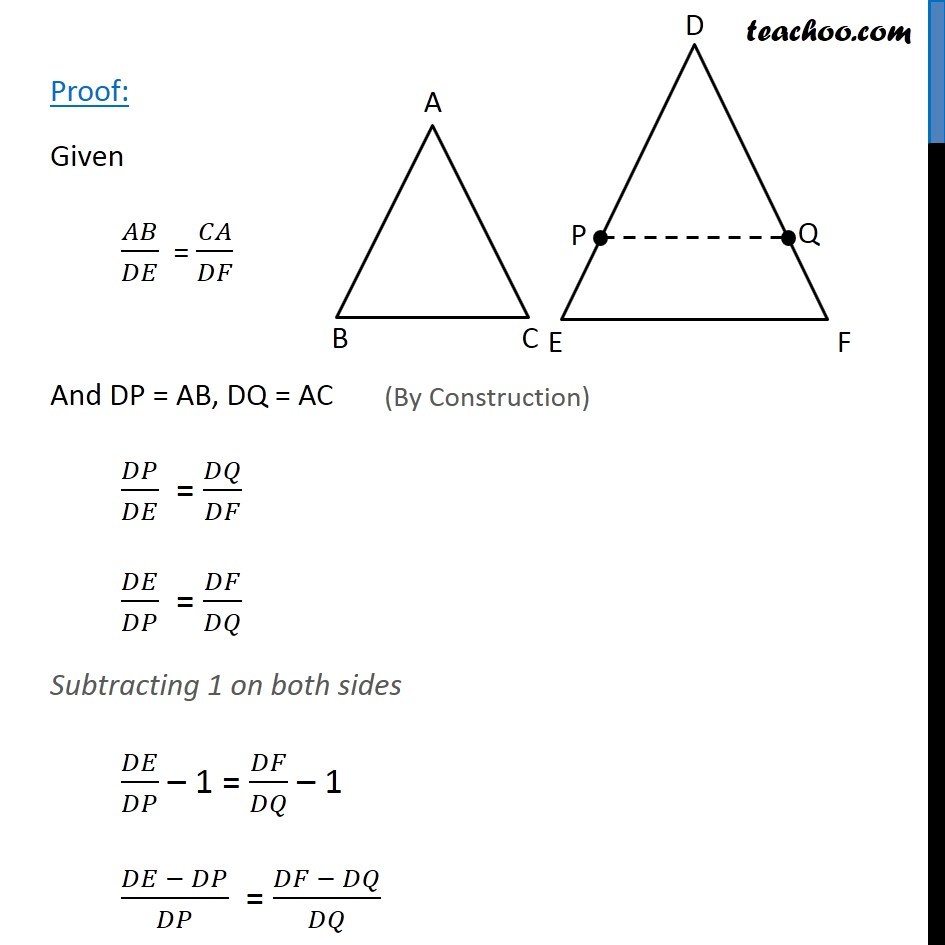
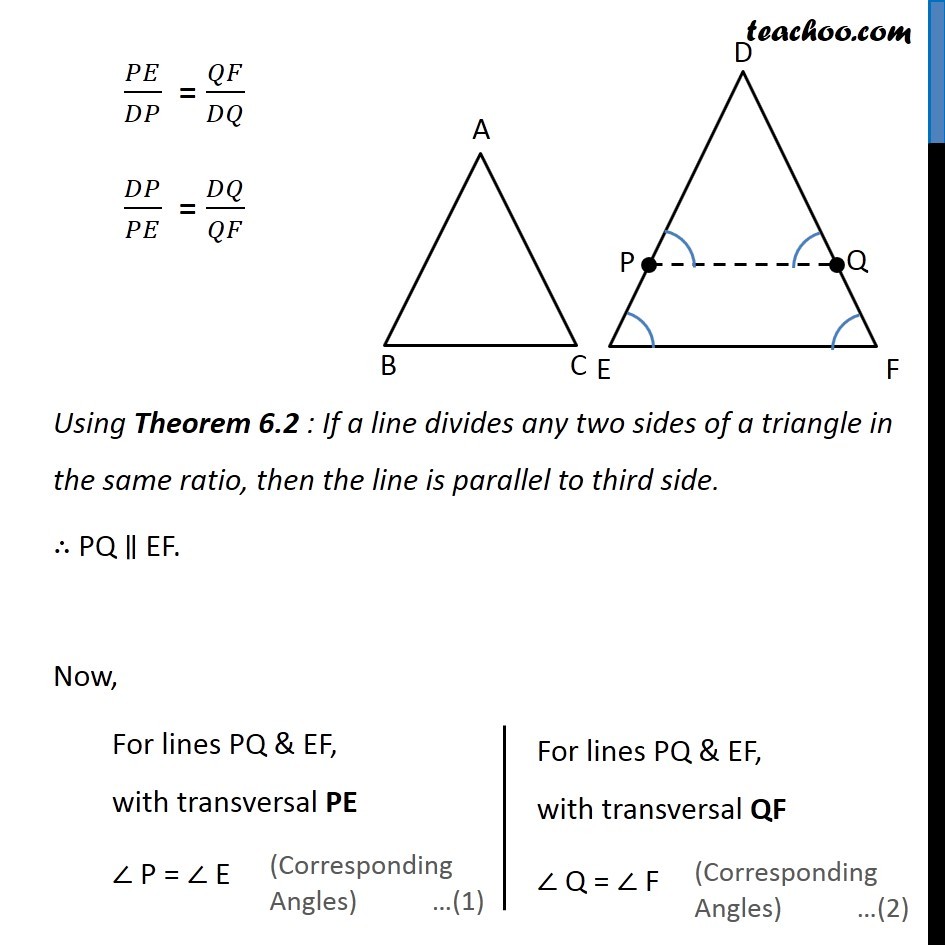
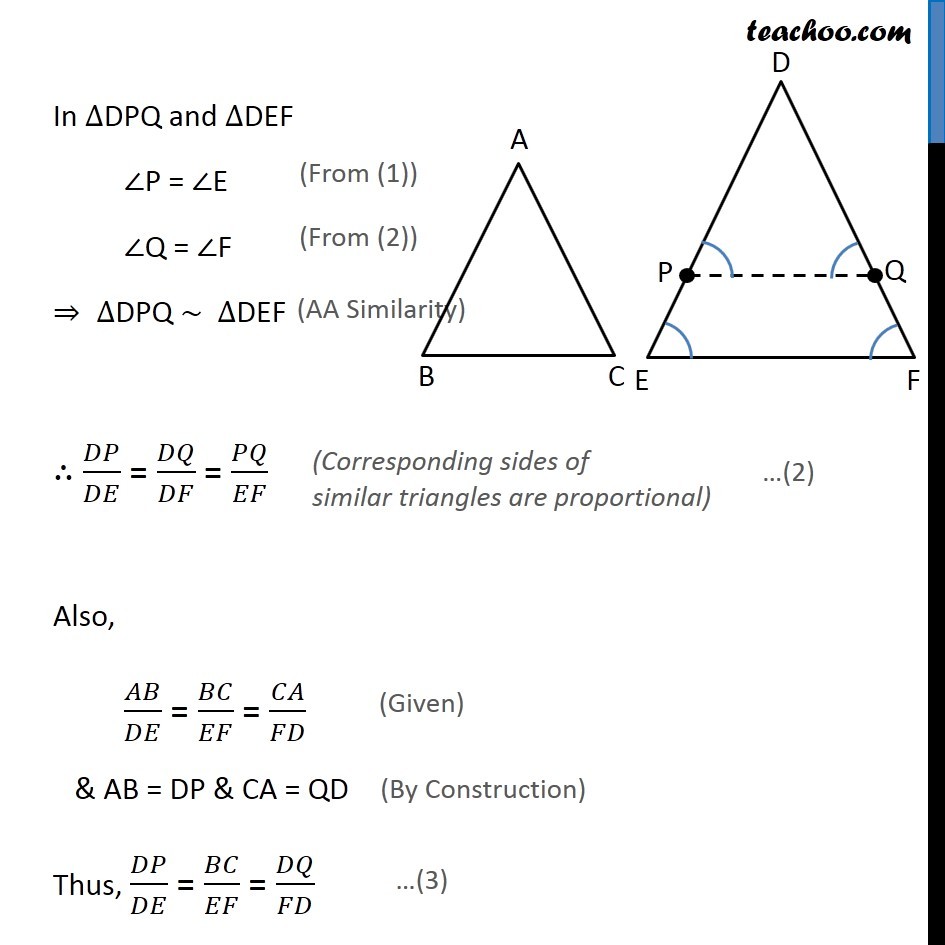
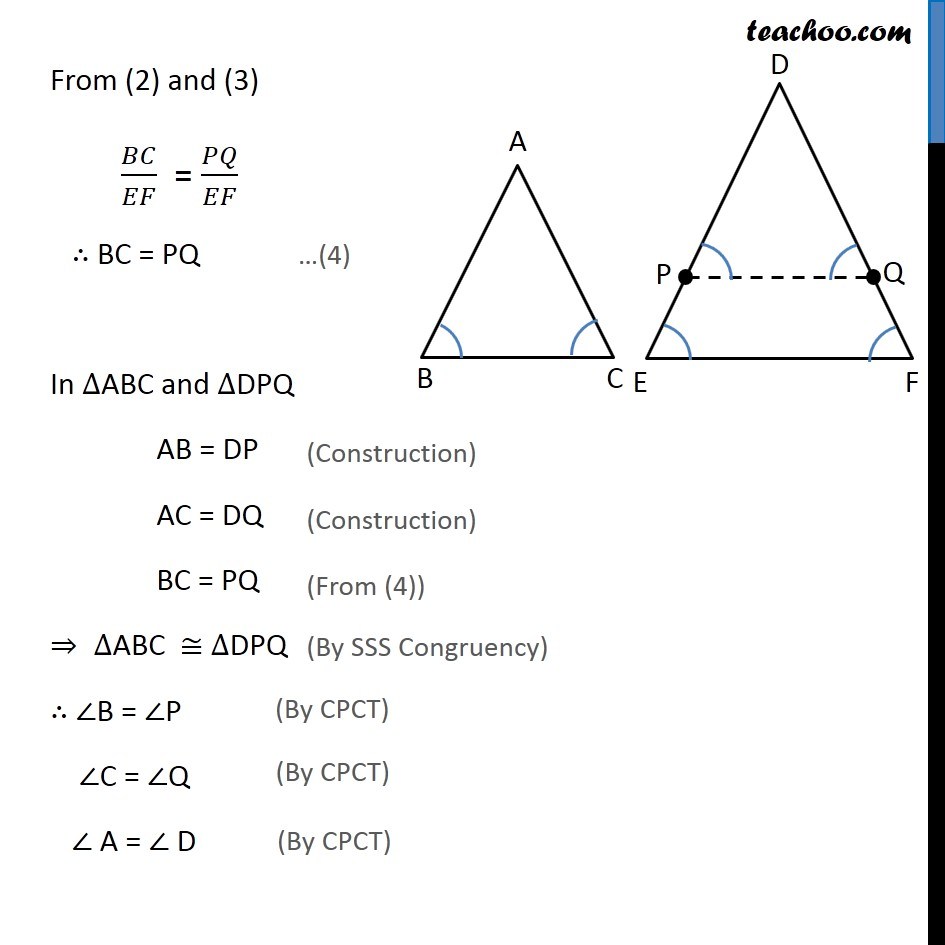
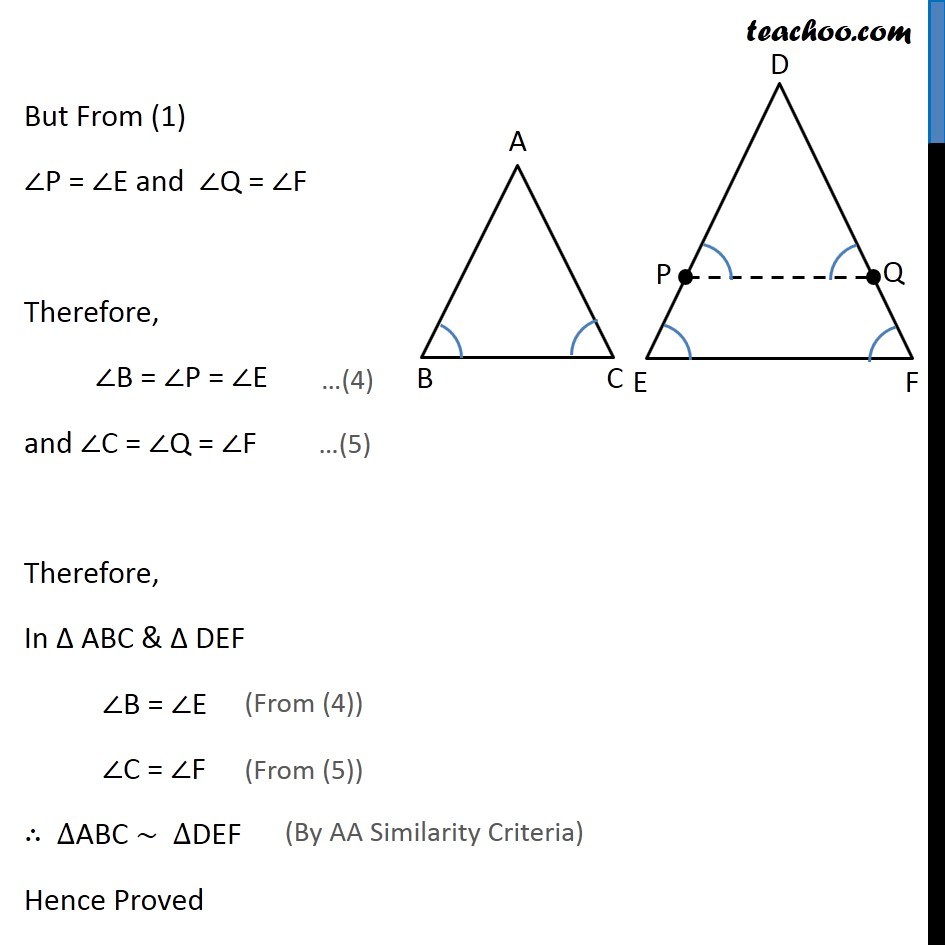
Theorem 6.4 (SSS Criteria) : If in two triangles, sides of one triangle are proportional to (i.e., the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangle are similar. Given: Triangle ∆ABC and ∆DEF such that 𝐴𝐵/𝐷𝐸 = 𝐵𝐶/𝐸𝐹 = 𝐶𝐴/𝐹𝐷 To Prove: ∠A = ∠D, ∠B = ∠E, ∠C = ∠F and ∆ABC ~ ∆DEF Construction: Draw P and Q on DE & DF such that DP = AB and DQ = AC respectively and join PQ. Proof: Given 𝐴𝐵/𝐷𝐸 = 𝐶𝐴/𝐷𝐹 And DP = AB, DQ = AC 𝐷𝑃/𝐷𝐸 = 𝐷𝑄/𝐷𝐹 𝐷𝐸/𝐷𝑃 = 𝐷𝐹/𝐷𝑄 Subtracting 1 on both sides 𝐷𝐸/𝐷𝑃 – 1 = 𝐷𝐹/𝐷𝑄 – 1 (𝐷𝐸 − 𝐷𝑃)/𝐷𝑃 = (𝐷𝐹 − 𝐷𝑄)/𝐷𝑄 𝑃𝐸/𝐷𝑃 = 𝑄𝐹/𝐷𝑄 𝐷𝑃/𝑃𝐸 = 𝐷𝑄/𝑄𝐹 Using Theorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to third side. ∴ PQ ∥ EF. Now, For lines PQ & EF, with transversal PE ∠ P = ∠ E For lines PQ & EF, with transversal QF ∠ Q = ∠ F In ∆DPQ and ∆DEF ∠P = ∠E ∠Q = ∠F ⇒ ∆DPQ ~ ∆DEF ∴ 𝐷𝑃/𝐷𝐸 = 𝐷𝑄/𝐷𝐹 = 𝑃𝑄/𝐸𝐹 Also, 𝐴𝐵/𝐷𝐸 = 𝐵𝐶/𝐸𝐹 = 𝐶𝐴/𝐹𝐷 & AB = DP & CA = QD Thus, 𝐷𝑃/𝐷𝐸 = 𝐵𝐶/𝐸𝐹 = 𝐷𝑄/𝐹𝐷 From (2) and (3) 𝐵𝐶/𝐸𝐹 = 𝑃𝑄/𝐸𝐹 ∴ BC = PQ In ∆ABC and ∆DPQ AB = DP AC = DQ BC = PQ ⇒ ∆ABC ≅ ∆DPQ ∴ ∠B = ∠P ∠C = ∠Q ∠ A = ∠ D But From (1) ∠P = ∠E and ∠Q = ∠F Therefore, ∠B = ∠P = ∠E and ∠C = ∠Q = ∠F Therefore, In Δ ABC & Δ DEF ∠B = ∠E ∠C = ∠F ∴ ∆ABC ~ ∆DEF Hence Proved