

Vector product - Area
Last updated at Dec. 16, 2024 by Teachoo



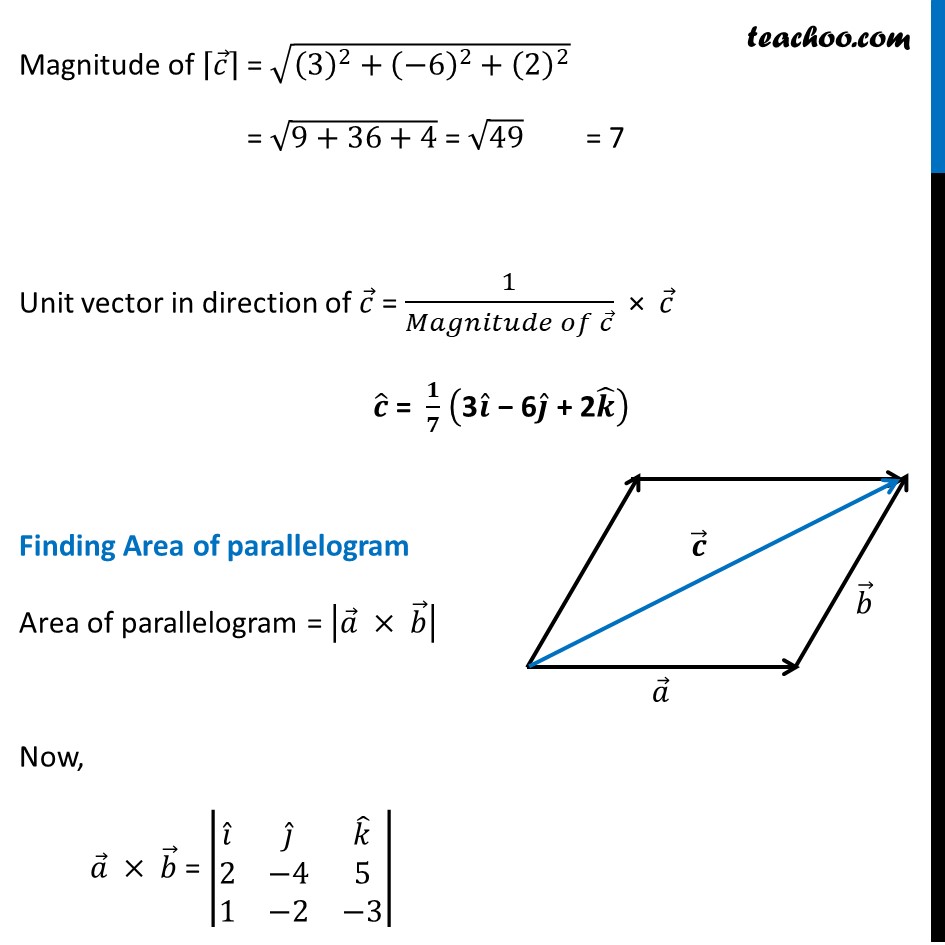
Transcript
Misc 10 The two adjacent sides of a parallelogram are 2𝑖 ̂ − 4𝑗 ̂ + 5𝑘 ̂ and 𝑖 ̂ − 2𝑗 ̂ − 3𝑘 ̂ Find the unit vector parallel to its diagonal. Also, find its area. Let 𝑎 ⃗ and 𝑏 ⃗ are adjacent side of a parallelogram, where 𝒂 ⃗ = 2𝑖 ̂ − 4𝑗 ̂ + 5𝑘 ̂ 𝒃 ⃗ = 𝑖 ̂ − 2𝑗 ̂ − 3𝑘 ̂ Let diagonal be 𝒄 ⃗ Hence, 𝒄 ⃗ = 𝒂 ⃗ + 𝒃 ⃗ = (2𝑖 ̂ − 4𝑗 ̂ + 5𝑘 ̂) + (1𝑖 ̂ − 2𝑗 ̂ − 3𝑘 ̂) = (2 + 1) 𝑖 ̂ − (4 + 2) 𝑗 ̂ + (5 − 3)𝑘 ̂ = 3𝒊 ̂ − 6𝒋 ̂ + 2𝒌 ̂ Magnitude of ⌈𝑐 ⃗ ⌉ = √((3)^2+(−6)^2+(2)^2 ) = √(9+36+4) = √49 = 7 Unit vector in direction of 𝑐 ⃗ = 1/(𝑀𝑎𝑔𝑛𝑖𝑡𝑢𝑑𝑒 𝑜𝑓 𝑐 ⃗ ) × 𝑐 ⃗ 𝒄 ̂ = 𝟏/𝟕 ("3" 𝒊 ̂" − 6" 𝒋 ̂" + 2" 𝒌 ̂ ) Finding Area of parallelogram Area of parallelogram = |𝑎 ⃗ × 𝑏 ⃗ | Now, 𝑎 ⃗ × 𝑏 ⃗ = |■8(𝑖 ̂&𝑗 ̂&𝑘 ̂@2&−4&5@1&−2&−3)| = 𝑖 ̂ (12 − (−10) − 𝑗 ̂ (−6 −5) + 𝑘 ̂ (−4 − (−4)) = 22𝑖 ̂ + 11𝑗 ̂ + 0𝑘 ̂ = 22𝑖 ̂ + 11𝑗 ̂ So 𝒂 ⃗ × 𝒃 ⃗ = 22𝒊 ̂ + 11𝒋 ̂ Now, |𝑎 ⃗ × 𝑏 ⃗ | = √(22^2+11^2 ) = √(2^2 (〖11)〗^2+11^2 ) = √( 11^2 (2^2+1)) = 11√5 Hence, Area of parallelogram = |𝑎 ⃗ × 𝑏 ⃗ |= 𝟏𝟏√𝟓