Question 11 - Figure it out - Page 196 to 198 - Chapter 8 Class 7 - Working with Fractions (Ganita Prakash)

Transcript

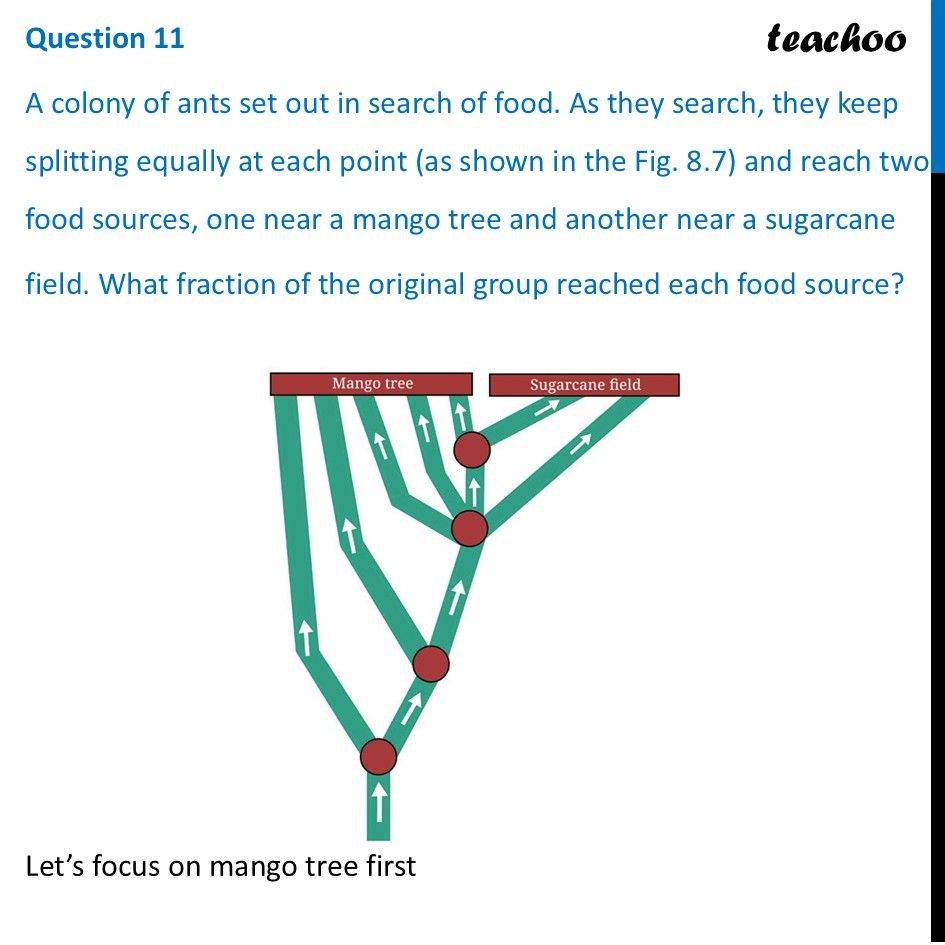
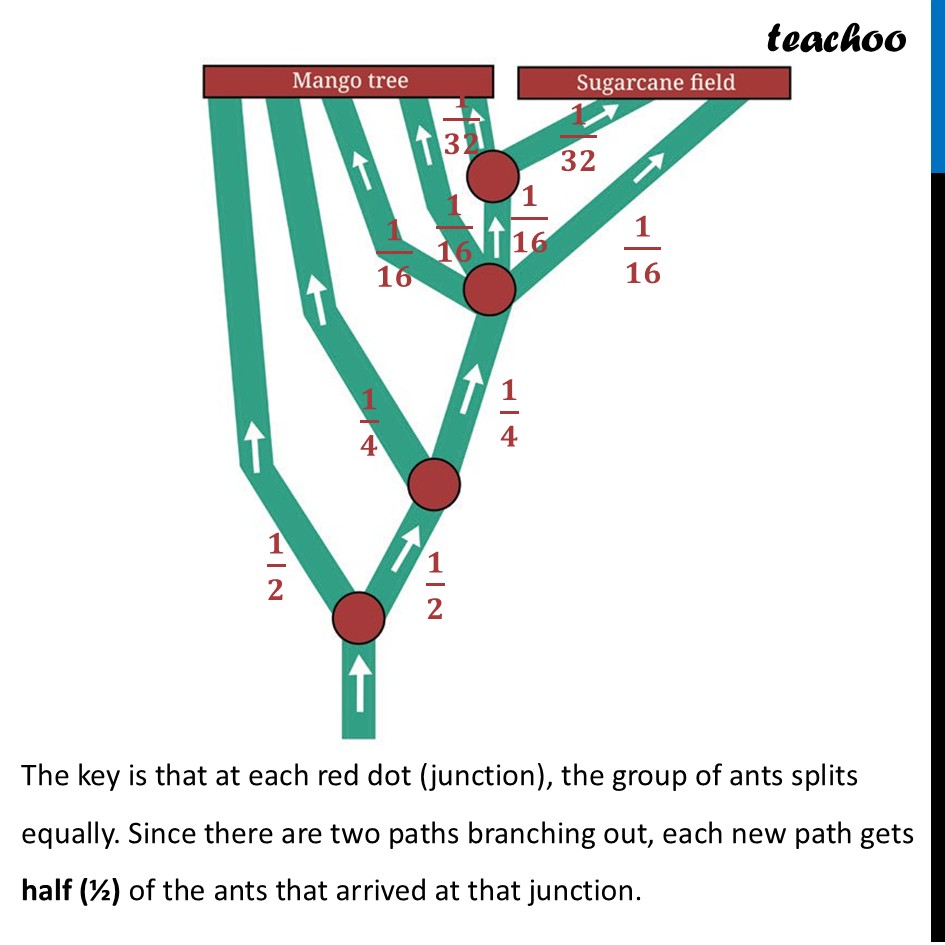
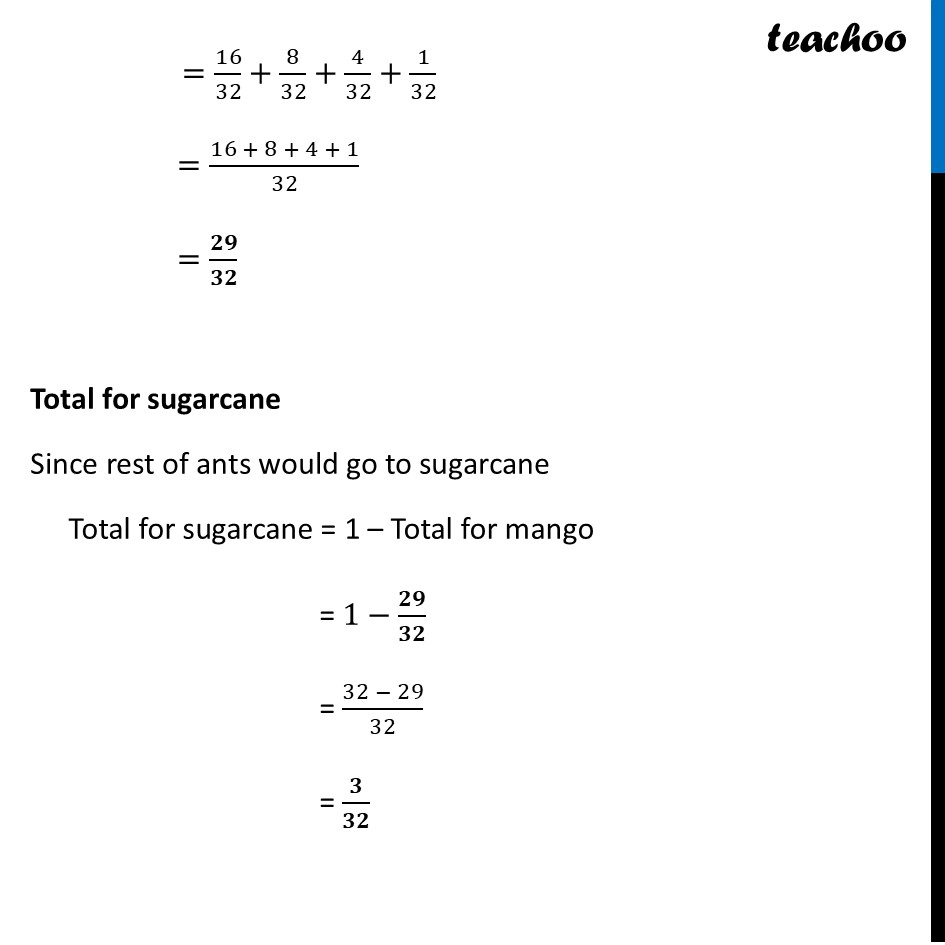
Question 11 A colony of ants set out in search of food. As they search, they keep splitting equally at each point (as shown in the Fig. 8.7) and reach two food sources, one near a mango tree and another near a sugarcane field. What fraction of the original group reached each food source? Let’s focus on mango tree first The key is that at each red dot (junction), the group of ants splits equally. Since there are two paths branching out, each new path gets half (½) of the ants that arrived at that junction. Now, First Junction: The group splits. Half go left, half go right. The left path gets ½ of the colony. Second Junction : This group of ½ splits again. The upper path to the mango tree gets half of this group. Calculation: 1/2 ×1/2=1/4​ . So, ¼ of the original colony reaches the mango tree via this path. Third Junction: Now this splits into 4 parts. And, two parts go into mango tree path leading left towards the mango tree gets half of this group. Calculation: 1/4 ×1/4=1/16 2 parts go to Mango, one goes to sugarcane, one goes to 4th junction Fourth Junction: This group splits into 2 parts. One path goes to mango tree, one goes to sugarcane Calculation: 1/2 ×1/16=1/32 Total for Mango Tree: We add the fractions from the two paths that end at the mango tree. 𝟏/𝟐+𝟏/𝟒+𝟏/𝟏𝟔+𝟏/𝟏𝟔+𝟏/𝟑𝟐 =1/2+1/4+(1/16+1/16)+1/32 =1/2+1/4+((1 + 1)/16)+1/32 =𝟏/𝟐+𝟏/𝟒+(𝟐/𝟏𝟔)+𝟏/𝟑𝟐 Here common denominator is 32 =1/2 ×16/16+1/4 ×8/8+2/16 ×2/2+1/32 =16/32+8/32+4/32+1/32 =(16 + 8 + 4 + 1)/32 =𝟐𝟗/𝟑𝟐 Total for sugarcane Since rest of ants would go to sugarcane Total for sugarcane = 1 – Total for mango = 1−𝟐𝟗/𝟑𝟐 = (32 − 29)/32 = 𝟑/𝟑𝟐 Therefore, 𝟐𝟗/𝟑𝟐 of the original group reached the mango tree. 𝟑/𝟑𝟐 of the original group reached the sugarcane field.