The angles of depression of the top and bottom of a 50m high building

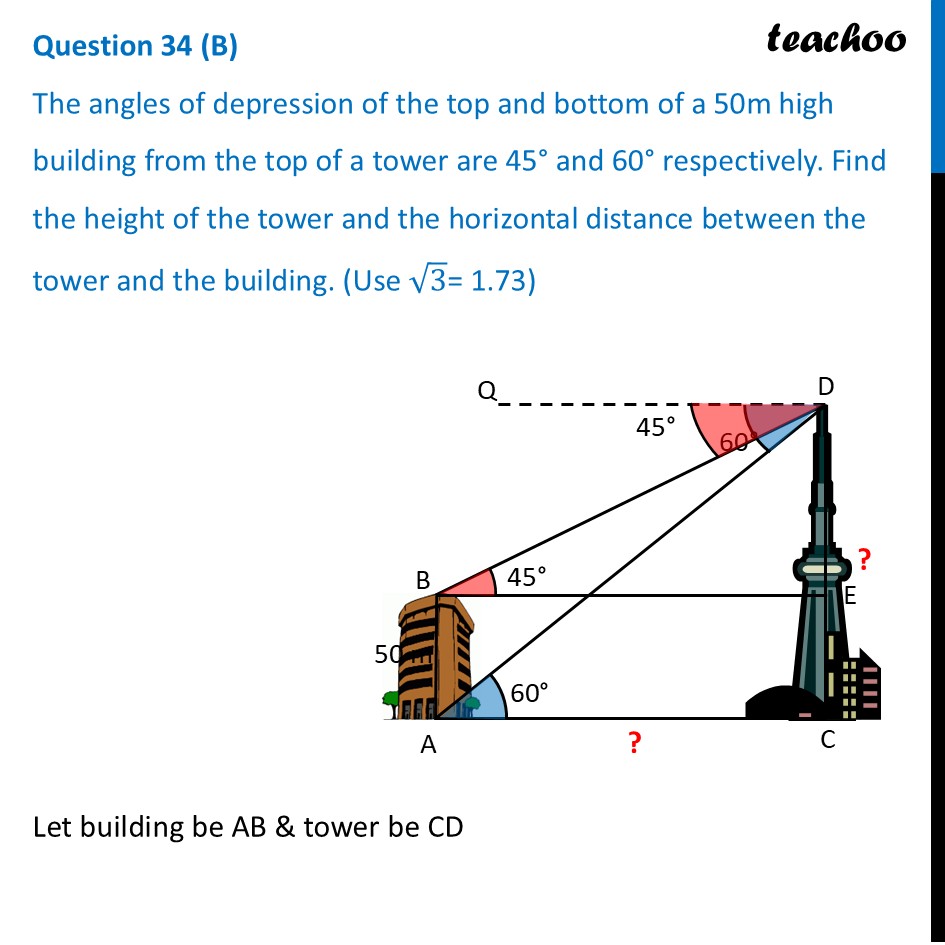
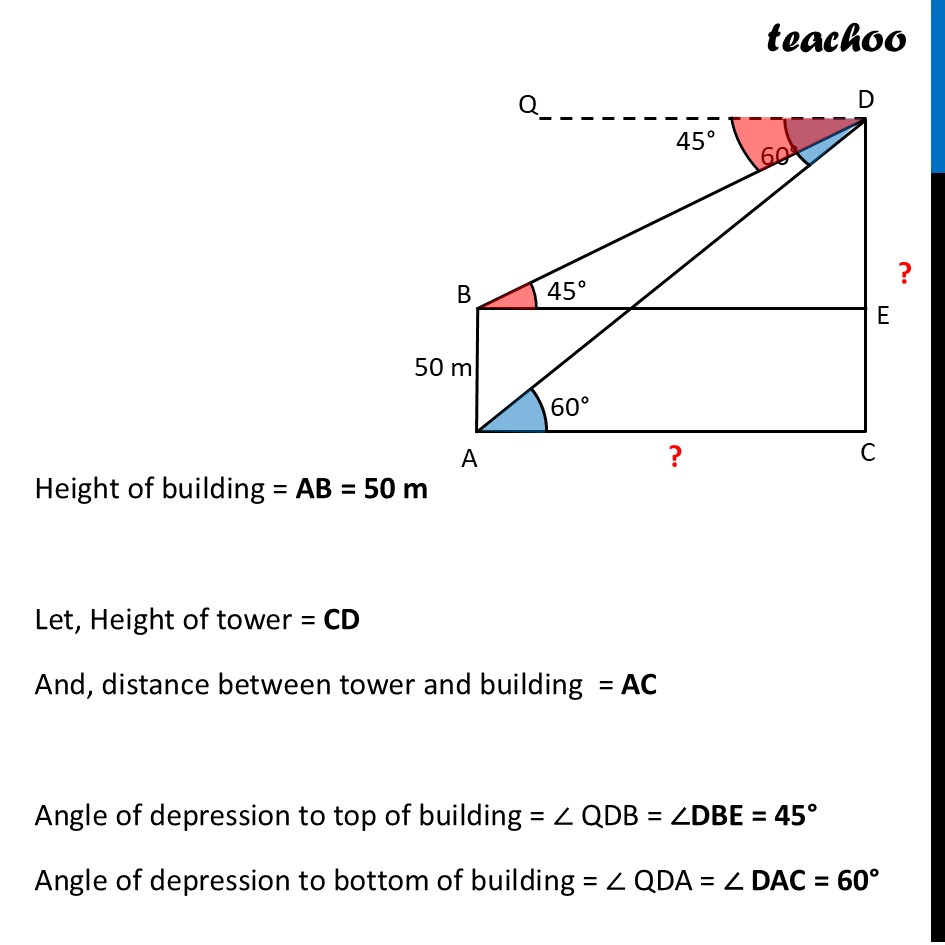
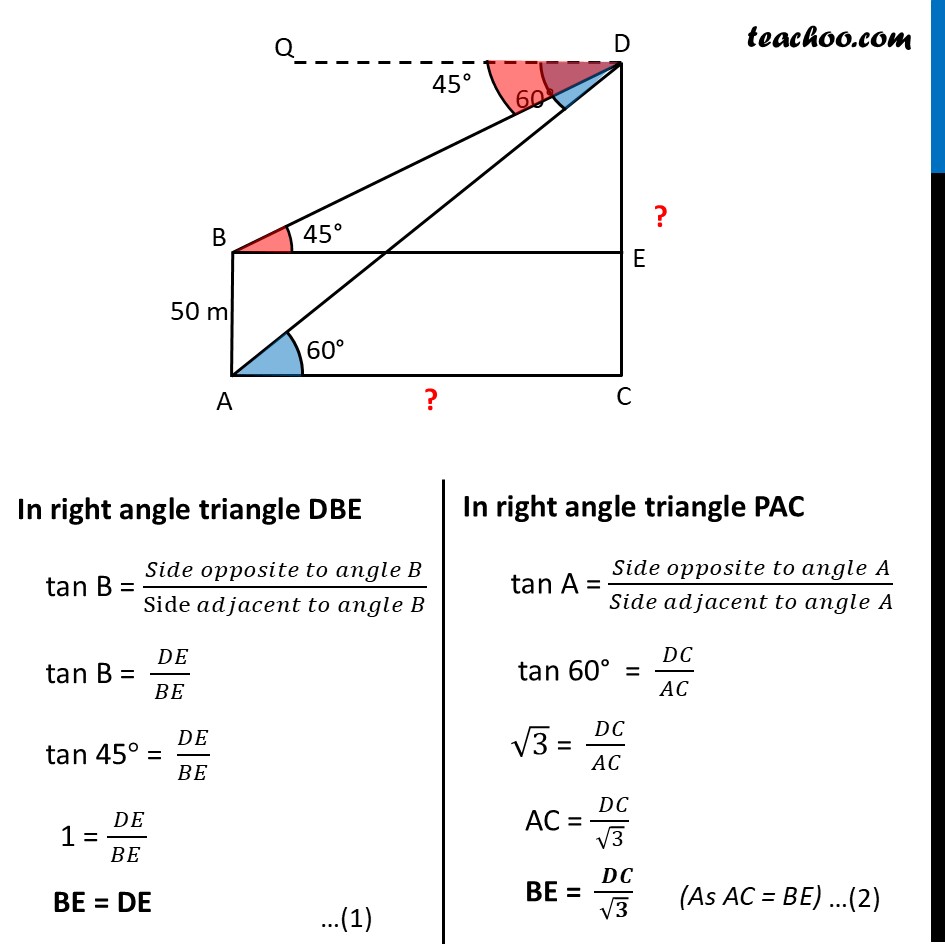
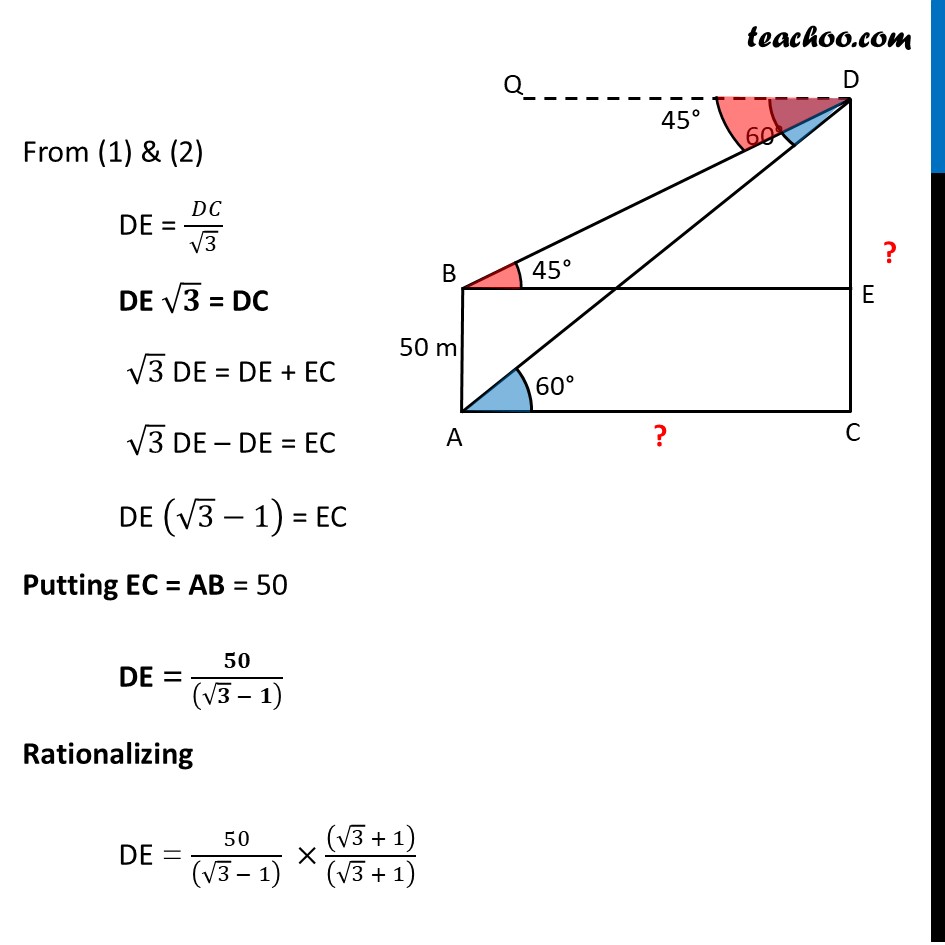
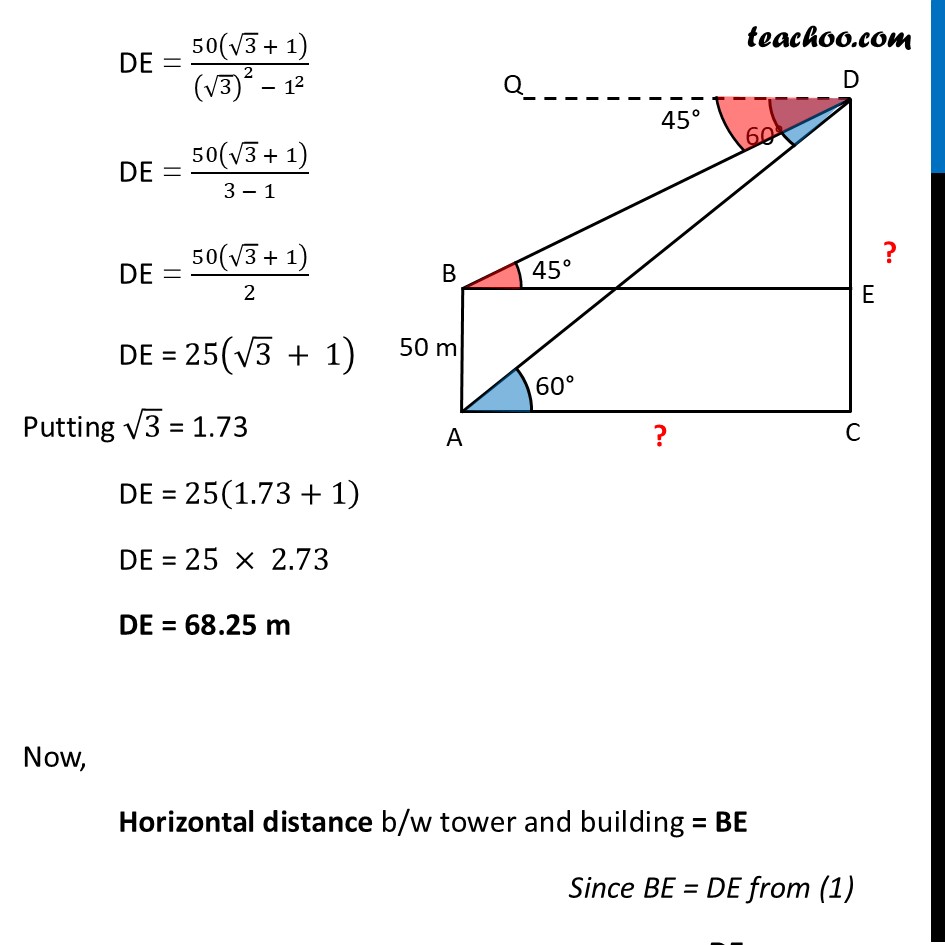
Question 34 (B) The angles of depression of the top and bottom of a 50m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building. (Use √3 "= 1.73")Let building be AB & tower be CD Height of building = AB = 50 m Let, Height of tower = CD And, distance between tower and building = AC Angle of depression to top of building = ∠ QDB = ∠DBE = 45° Angle of depression to bottom of building = ∠ QDA = ∠ DAC = 60° In right angle triangle DBE tan B = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝐵)/(Side 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐵) tan B = (" " 𝐷𝐸)/𝐵𝐸 tan 45° = 𝐷𝐸/𝐵𝐸 1 = (" " 𝐷𝐸)/𝐵𝐸 BE = DE In right angle triangle PAC tan A = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐴)/(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐴) tan 60° = (" " 𝐷𝐶)/𝐴𝐶 √3 = (" " 𝐷𝐶)/𝐴𝐶 AC = (" " 𝐷𝐶)/√3 "BE = " (" " 𝑫𝑪)/√𝟑 From (1) & (2) DE = (" " 𝐷𝐶)/√3 DE √𝟑 = DC √3 DE = DE + EC √3 DE – DE = EC DE (√3−1) = EC Putting EC = AB = 50 DE = 𝟓𝟎/((√𝟑 − 𝟏) ) Rationalizing DE = 50/((√3 − 1) ) ×((√3 + 1))/((√3 + 1) ) DE = 50(√3 + 1)/((√3)^2 − 1^2 ) DE = 50(√3 + 1)/(3 − 1) DE = 50(√3 + 1)/2 DE = 25(√3 + 1) Putting √3 = 1.73 DE = 25(1.73+1) DE = 25 × 2.73 DE = 68.25 m Now, Horizontal distance b/w tower and building = BE Since BE = DE from (1) = DE = 68.25 m And, Height of tower = CD = DE + EC Putting EC = AB = 68.25 + 50 = 118.25 m

Question 34 (B) - CBSE Class 10 Sample Paper for 2026 Boards - Maths Basic - Solutions of Sample Papers for Class 10 Boards

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular