Question 22 - CBSE Class 10 Sample Paper for 2026 Boards - Maths Basic - Solutions of Sample Papers for Class 10 Boards

Last updated at September 10, 2025 by Teachoo

Find the radius of the circle with centre at origin, if line 𝑙 given - CBSE Class 10 Sample Paper for 2026 Boards - Maths Basic

part 2 - Question 22 - CBSE Class 10 Sample Paper for 2026 Boards - Maths Basic - Solutions of Sample Papers for Class 10 Boards - Class 10

part 3 - Question 22 - CBSE Class 10 Sample Paper for 2026 Boards - Maths Basic - Solutions of Sample Papers for Class 10 Boards - Class 10

Next: Question 23 → Remove Ads Share on WhatsApp

Transcript

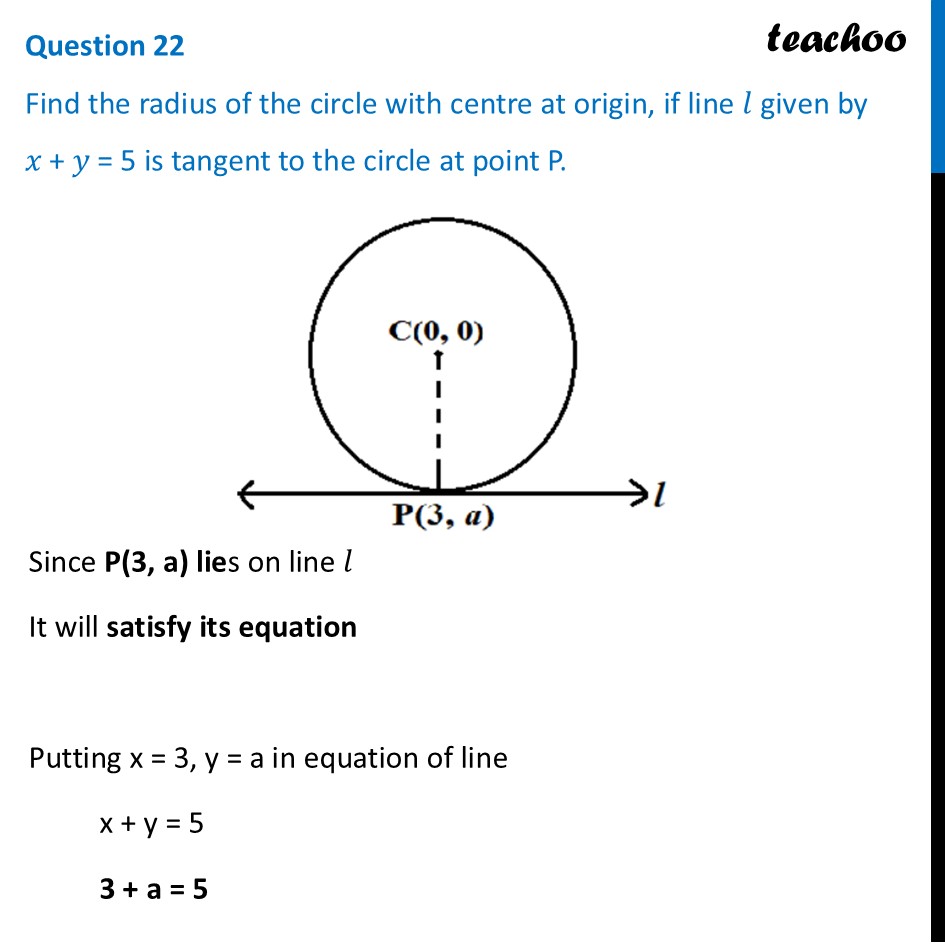
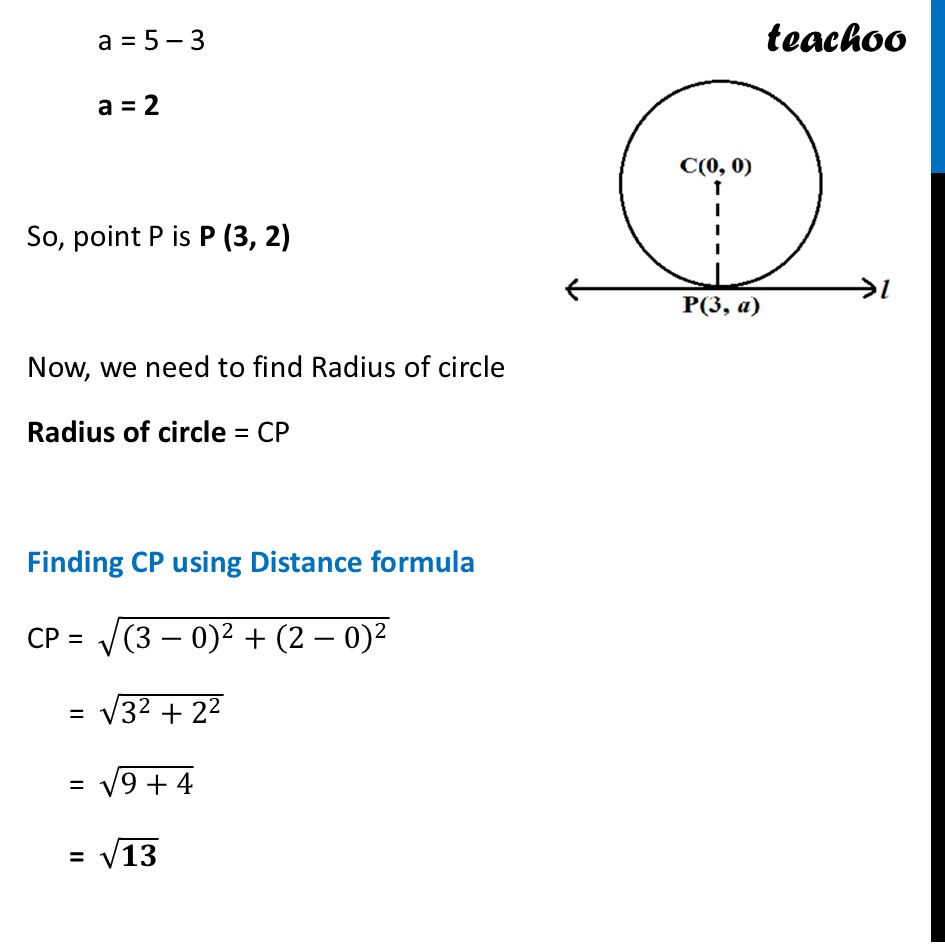
Question 22 Find the radius of the circle with centre at origin, if line 𝑙 given by 𝑥 + 𝑦 = 5 is tangent to the circle at point P.Since P(3, a) lies on line 𝑙 It will satisfy its equation Putting x = 3, y = a in equation of line x + y = 5 3 + a = 5 a = 5 – 3 a = 2 So, point P is P (3, 2) Now, we need to find Radius of circle Radius of circle = CP Finding CP using Distance formula CP = √((3−0)^2+(2−0)^2 ) = √(3^2+2^2 ) = √(9+4) = √𝟏𝟑 Thus, radius of circle is √𝟏𝟑 units

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 15 years. He provides courses for Maths, Science and Computer Science at Teachoo

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular