Question 2 - Examples - Chapter 12 Class 10 Surface Areas and Volumes

Transcript

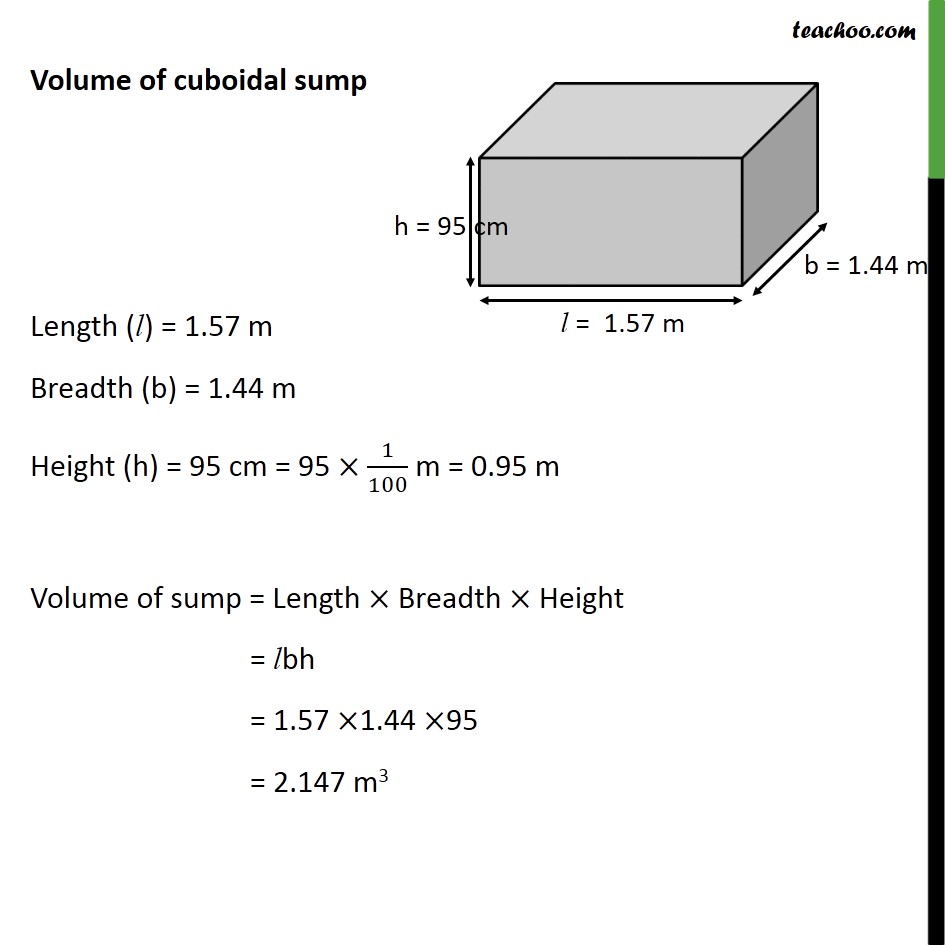
Question 2 Selvi s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m 1.44 m 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use = 3.14) Lets first find volume of water left in sump Volume of water left in the cuboidal sump after filling the tank = Volume of cuboidal sump Volume of cylindrical tank Volume of cuboidal sump Length (l) = 1.57 m Breadth (b) = 1.44 m Height (h) = 95 cm = 95 1/100 m = 0.95 m Volume of sump = Length Breadth Height = lbh = 1.57 1.44 95 = 2.147 m3 Volume of overhead tank Height of overhead tank = h = 95 cm = 95 1/100 m = 0.95 m And, radius = r = 60 cm= 60 1/100 m = 0.6 m Volume of overhead tank = 2 = (0.6)2 (0.95) = 0.342 m3 = 0.342 3.14 = 1.074 m3 Volume of water left in the cuboidal sump after filling the tank = Volume of cuboidal sump Volume of cylindrical tank = 2.147 1.073 = 1.073 m3 Now, Volume of water left in cuboidal sump = 1.073 Length Breadth Height = 1.73 1.57 1.44 h = 1.073 h = 1.073/(1.57 1.44) h = 0.475 m h = 0.475 100 cm h = 47.5 cm So, height of water left in sump = 47.5 cm Also, ( )/( ) = ( )/( ) = 1.073/2.147 = 0.499 = 0.5 (approximately) = 5/10 = 1/2 Hence, capacity of the tank is half the capacity of the sump .