Question 10 - Important Area Questions - Chapter 11 Class 10 Areas related to Circles

Transcript

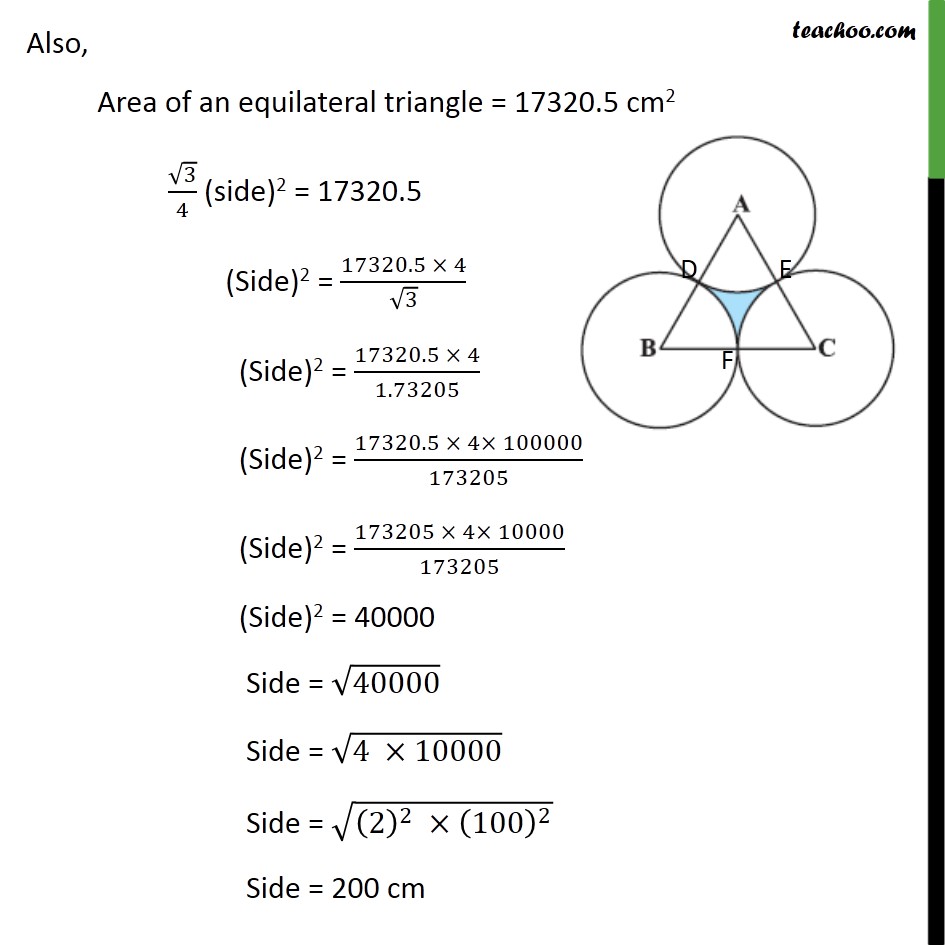
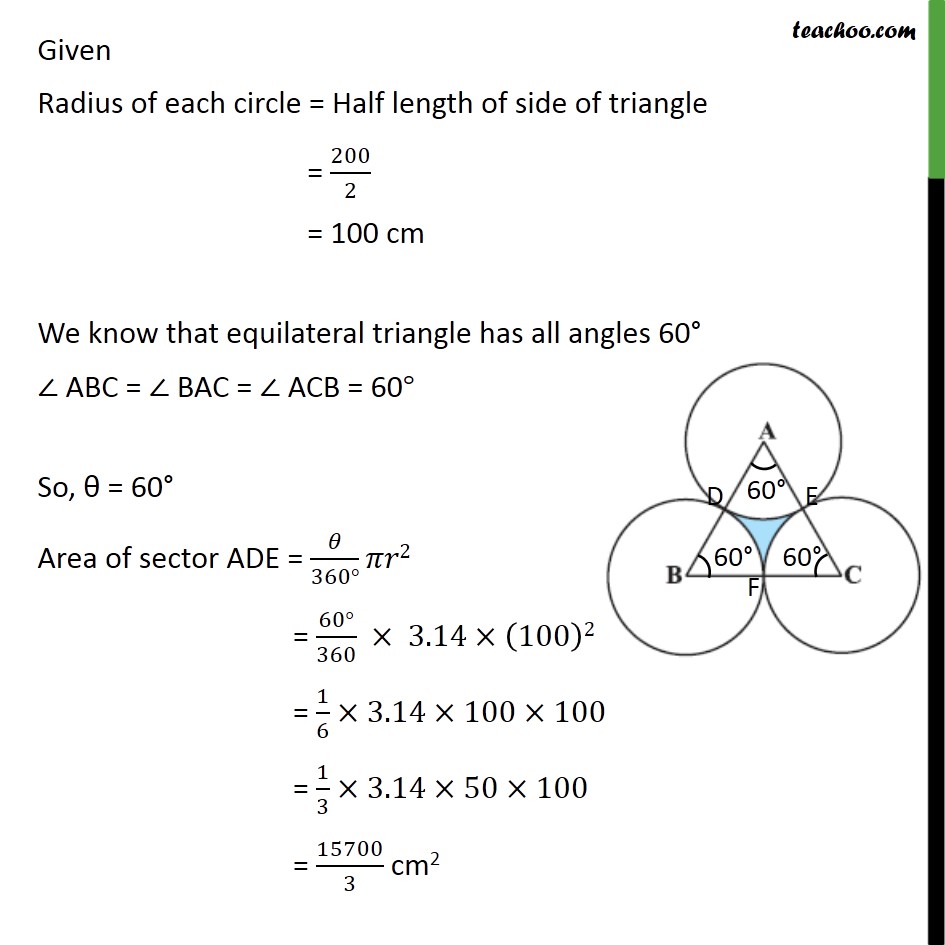
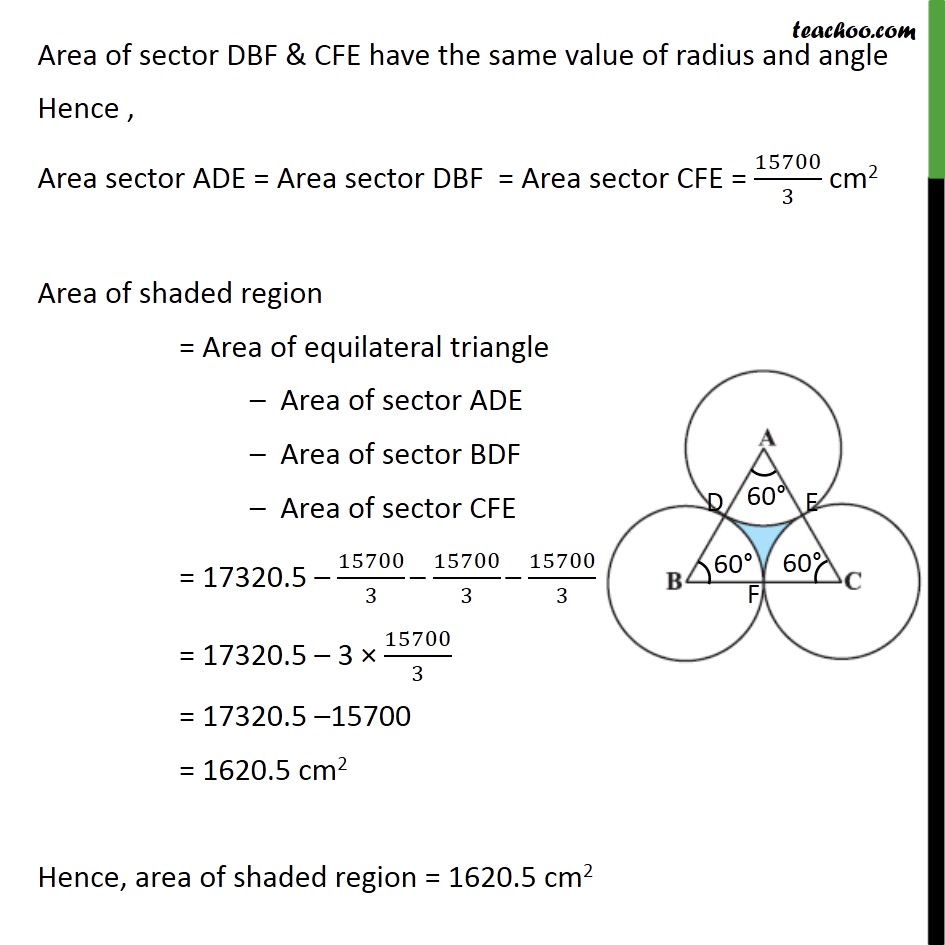
Question 10 The area of an equilateral triangle ABC is 17320.5 cm2 . With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region. (Use = 3.14 and 3= 1.73205) Area of shaded region = Area of equilateral triangle Area of sector ADE Area of sector BDF Area of sector CFE It is given that, ABC is an equilateral triangle, So, sides of an triangle = AB = BC = AC Also, Area of an equilateral triangle = 17320.5 cm2 3/4 (side)2 = 17320.5 (Side)2 = (17320.5 4)/ 3 (Side)2 = (17320.5 4)/1.73205 (Side)2 = (17320.5 4 100000)/173205 (Side)2 = (173205 4 10000)/173205 (Side)2 = 40000 Side = 40000 Side = (4 10000) Side = ((2)^2 (100)^2 ) Side = 200 cm Given Radius of each circle = Half length of side of triangle = 200/2 = 100 cm We know that equilateral triangle has all angles 60 ABC = BAC = ACB = 60 So, = 60 Area of sector ADE = /(360 ) 2 = (60 )/360 3.14 (100)2 = 1/6 3.14 100 100 = 1/3 3.14 50 100 = 15700/3 cm2 Area of sector DBF & CFE have the same value of radius and angle Hence , Area sector ADE = Area sector DBF = Area sector CFE = 15700/3 cm2 Area of shaded region = Area of equilateral triangle Area of sector ADE Area of sector BDF Area of sector CFE = 17320.5 15700/3 15700/3 15700/3 = 17320.5 3 15700/3 = 17320.5 15700 = 1620.5 cm2 Hence, area of shaded region = 1620.5 cm2