Question 9 - Important Area Questions - Chapter 11 Class 10 Areas related to Circles

Transcript

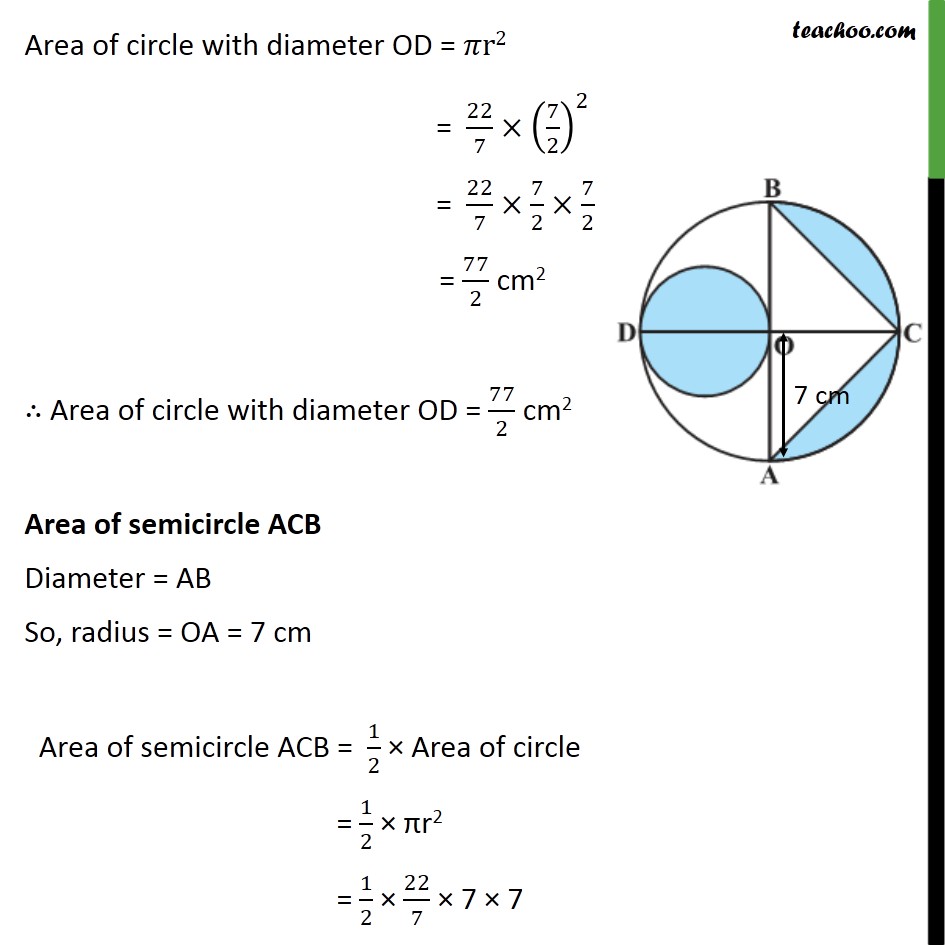
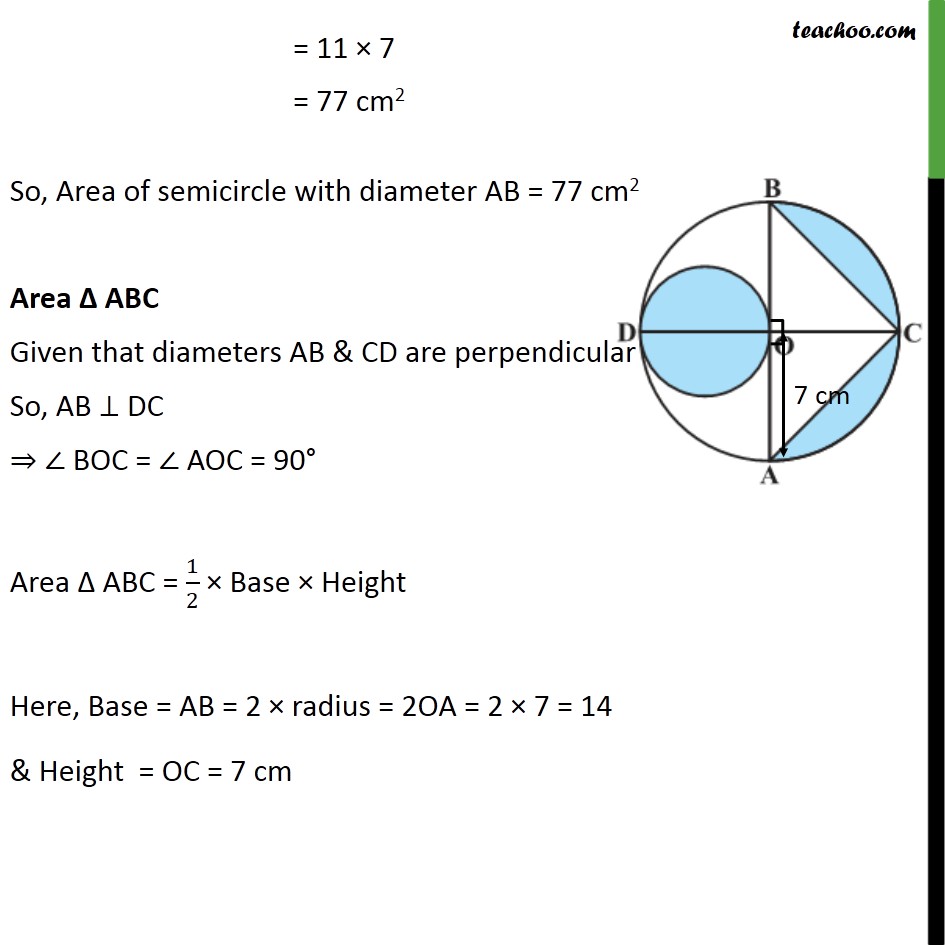
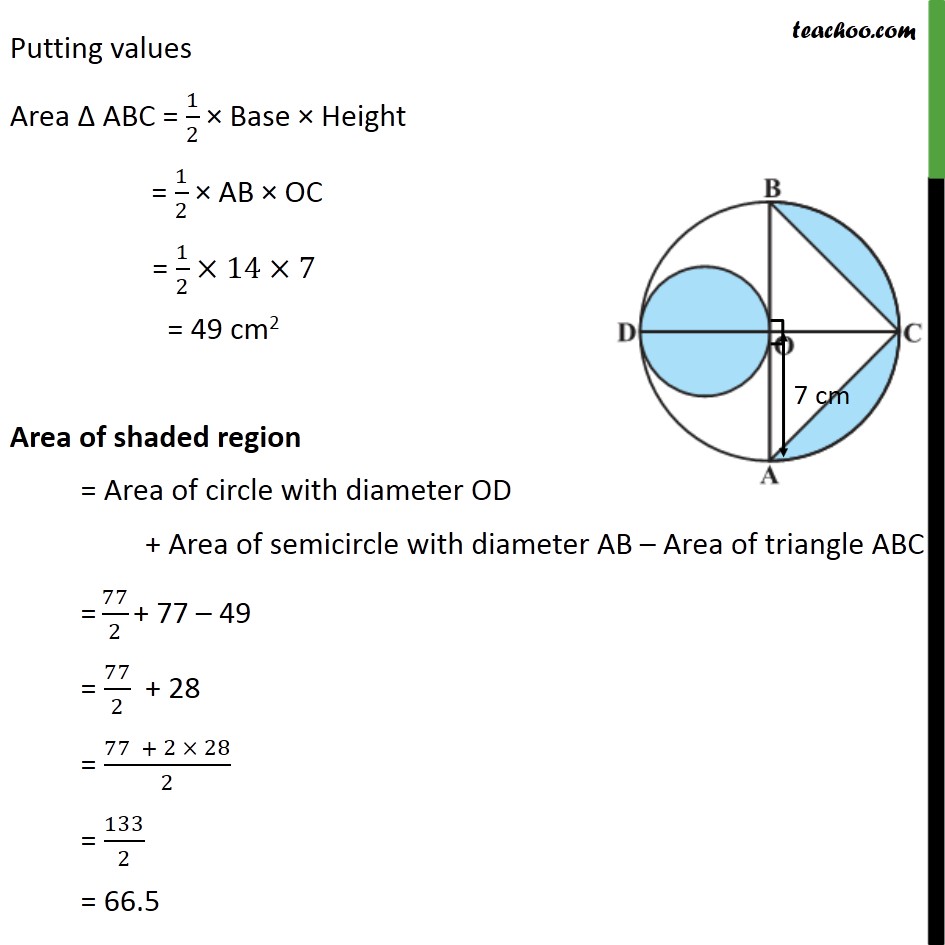
Question 9 In figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. Area of shaded region = Area of circle with diameter OD + Area of semicircle ACB Area of triangle ABC Area of circle with diameter OD Since OD & OA are radius of circle with centre O OD = OA = 7 cm Diameter = OD = 7 cm radius = r = /2 = 7/2 cm Area of circle with diameter OD = r2 = 22/7 (7/2)^2 = 22/7 7/2 7/2 = 77/2 cm2 Area of circle with diameter OD = 77/2 cm2 Area of semicircle ACB Diameter = AB So, radius = OA = 7 cm Area of semicircle ACB = 1/2 Area of circle = 1/2 r2 = 1/2 22/7 7 7 = 11 7 = 77 cm2 So, Area of semicircle with diameter AB = 77 cm2 Area ABC Given that diameters AB & CD are perpendicular So, AB DC BOC = AOC = 90 Area ABC = 1/2 Base Height Here, Base = AB = 2 radius = 2OA = 2 7 = 14 & Height = OC = 7 cm Putting values Area ABC = 1/2 Base Height = 1/2 AB OC = 1/2 14 7 = 49 cm2 Area of shaded region = Area of circle with diameter OD + Area of semicircle with diameter AB Area of triangle ABC = 77/2 + 77 49 = 77/2 + 28 = (77 + 2 28)/2 = 133/2 = 66.5