Question 4 - Important Area Questions - Chapter 11 Class 10 Areas related to Circles

Transcript

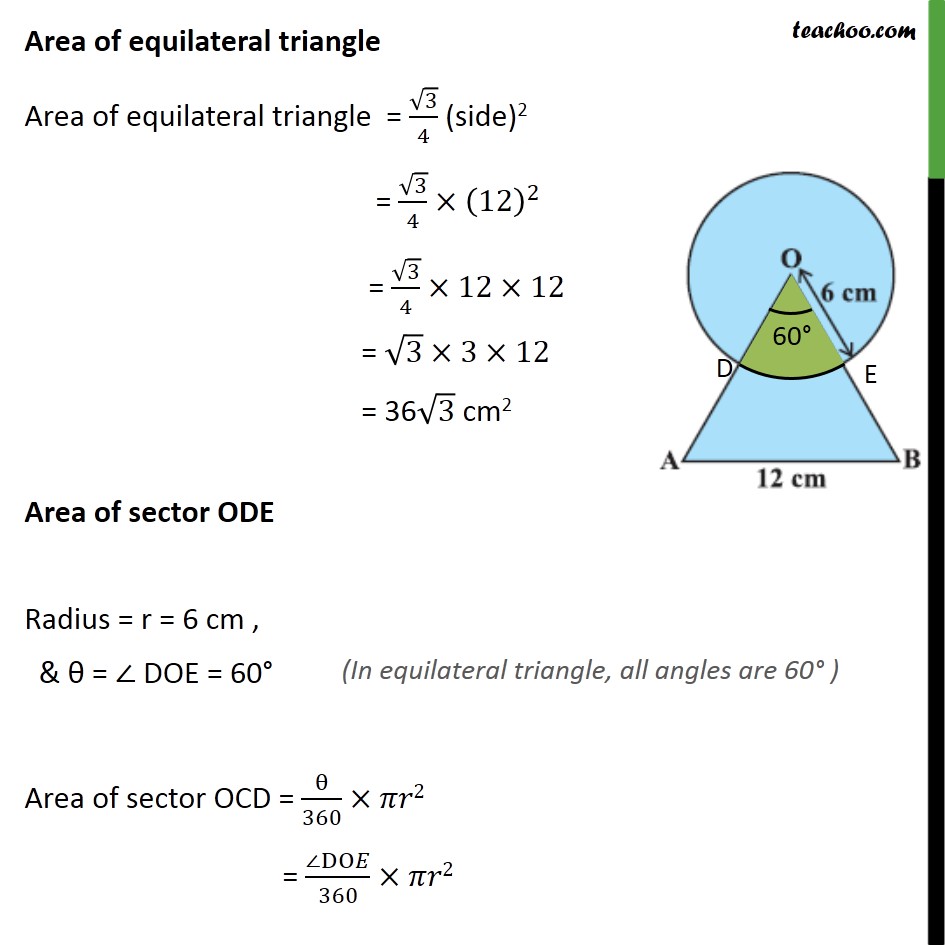
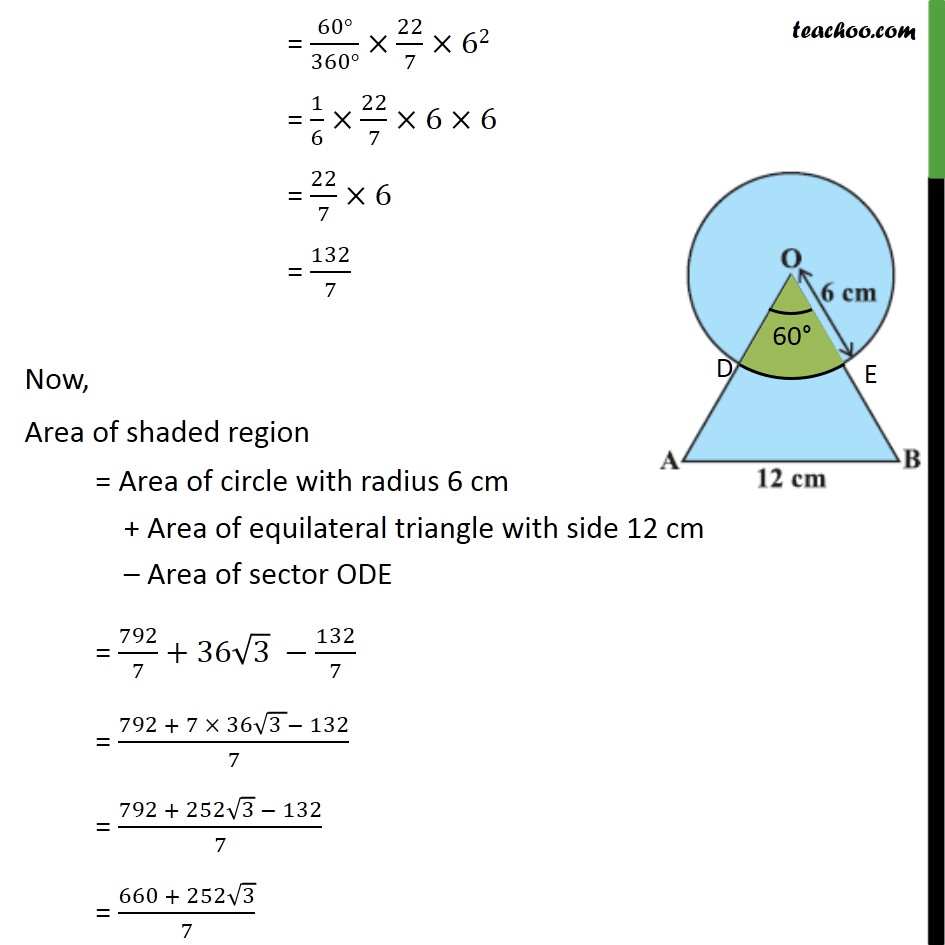
Question 4 Find the area of the shaded region in figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre. Area of shaded region = Area of circle with radius 6 cm + Area of equilateral triangle with side 12 cm – Area of sector ODE Area of circle Radius of circle = r = 6 cm Area of circle = 𝜋r2 = 22/7×(6)2 = 22/7 × 36 = 792/7 cm2 Area of equilateral triangle Area of equilateral triangle = √3/4 (side)2 = √3/4×(12)^2 = √3/4×12×12 = √3×3×12 = 36√3 cm2 Area of sector ODE Radius = r = 6 cm , & θ = ∠ DOE = 60° Area of sector OCD = θ/360×𝜋𝑟2 = (∠DO𝐸)/360×𝜋𝑟2 = (60°)/(360°)×22/7×62 = 1/6×22/7×6×6 = 22/7×6 = 132/7 Now, Area of shaded region = Area of circle with radius 6 cm + Area of equilateral triangle with side 12 cm – Area of sector ODE = 792/7+36√3 −132/7 = (792 + 7 × 36√(3 )− 132)/7 = (792 + 252√3 − 132)/7 = (660 + 252√3)/7 = 660/7 + (252√3)/7 = (660/7 +36√3) cm2 Hence, area of shaded region = (660/7+36√3) cm2