Ex 7.1, 6 (i) - Chapter 7 Class 10 Coordinate Geometry (Term 1)

Transcript

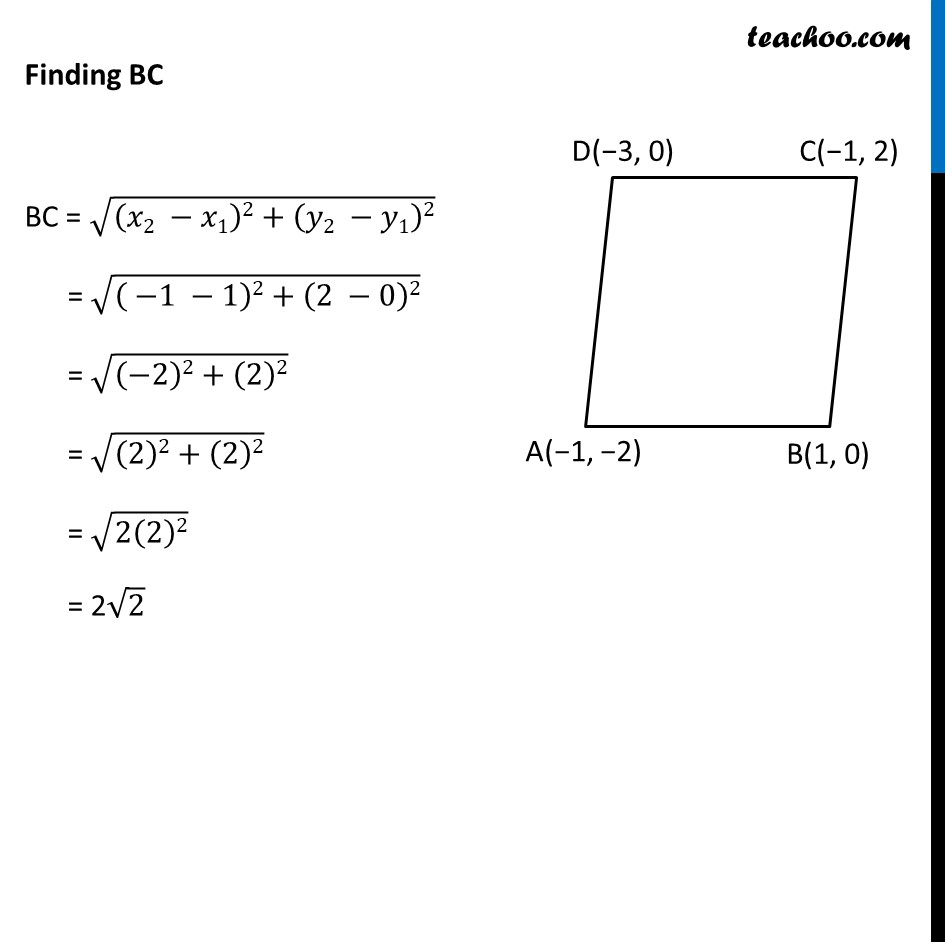
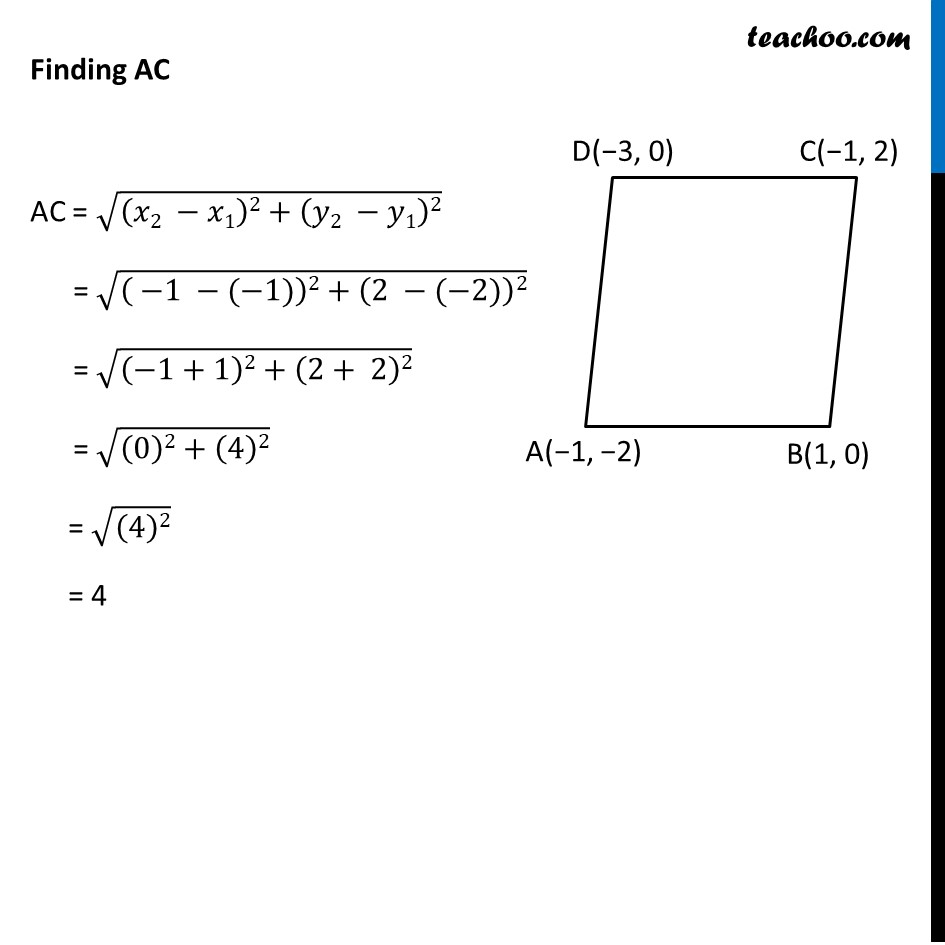
Ex 7.1, 6 Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer: (i) (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0) Let the points be A(−1, −2), B(1, 0), C(−1, 2), D(−3, 0) We find the distances AB, BC, CD & AD By using distance formula Finding AB AB = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 1 −(−1))2+(0 −(−2))2) = √((1+1)2+(0+2)2) = √((2)2+(2)2) = √(2(2)2) = 2√2 Finding BC BC = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −1 −1)2+(2 −0)2) = √((−2)2+(2)2) = √((2)2+(2)2) = √(2(2)2) = 2√2 Finding BC BC = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −1 −1)2+(2 −0)2) = √((−2)2+(2)2) = √((2)2+(2)2) = √(2(2)2) = 2√2 Finding CD CD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −3 −(−1))2+(0 −2)2) = √((−3+1)2+(−2)2) = √((−2)2+(−2)2) = √((2)2+(2)2) = √(2(2)2) = 2√2 Finding CD CD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −3 −(−1))2+(0 −2)2) = √((−3+1)2+(−2)2) = √((−2)2+(−2)2) = √((2)2+(2)2) = √(2(2)2) = 2√2 Finding AD AD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −3 −(−1))2+(0 −(−2))2) = √((−3+1)2+(2)2) = √((−2)2+(2)2) = √((2)2+(2)2) = √(2(2)2) = 2√2 Since, AB = BC = CD = AD = 2√2 All sides of quadrilateral are equal, ∴ It can be a rhombus or a square. To check if it is a square, we find diagonals AC and BD Finding AC AC = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( −1 −(−1))2+(2 −(−2))2) = √((−1+1)2+(2+ 2)2) = √((0)2+(4)2) = √((4)2) = 4 Now, Finding BD BD = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 1 −(−3))2+(0 −0)2) = √(( 1+3)2+(0)2) = √((4)2+(0)2) = √((4)2) = 4 Since, AB = BC = CD = AD = 2√2 All sides of quadrilateral are equal, & AC = BD = 4 Hence, both diagonals are equal Since, all sides and both diagonals are equal ABCD is a square