Ex 7.1, 4 - Chapter 7 Class 10 Coordinate Geometry

Transcript

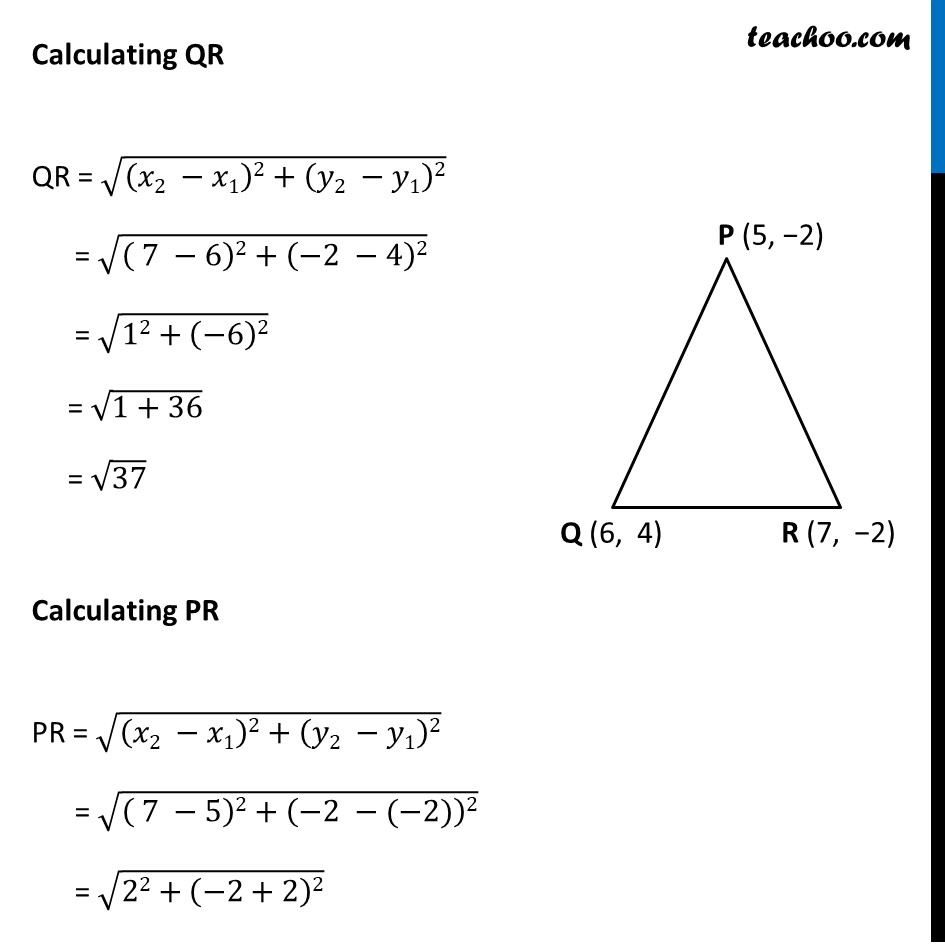
Ex 7.1, 4 Check whether (5, –2), (6, 4) and (7, –2) are the vertices of an isosceles triangle. In an isosceles triangle, any 2 of the 3 sides are equal. Let the three points be P(5, −2), Q(6, 4) & R(7, −2) In order to be isosceles, Either PQ = PR or PQ = QR or PR = QR We calculate the value of PQ, QR & PR by distance formula Calculating PQ PQ = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 6 −5)2+(4 −(−2))2) = √(12+(6)2) = √(1+36) = √37 Calculating QR QR = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 7 −6)2+(−2 −4)2) = √(12+(−6)2) = √(1+36) = √37 Calculating PR PR = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 7 −5)2+(−2 −(−2))2) = √(22+(−2+2)2) Calculating QR QR = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 7 −6)2+(−2 −4)2) = √(12+(−6)2) = √(1+36) = √37 Calculating PR PR = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 7 −5)2+(−2 −(−2))2) = √(22+(−2+2)2) Calculating QR QR = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 7 −6)2+(−2 −4)2) = √(12+(−6)2) = √(1+36) = √37 Calculating PR PR = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) = √(( 7 −5)2+(−2 −(−2))2) = √(22+(−2+2)2) = √(2^2+0^2 ) = √(2^2 ) = 2 Hence, PQ = √37, QR = √37, PR = 2 Since PQ = QR It satisfies the condition of isosceles triangle Hence, PQR is an isosceles triangle