Ex 7.1, 2

Transcript

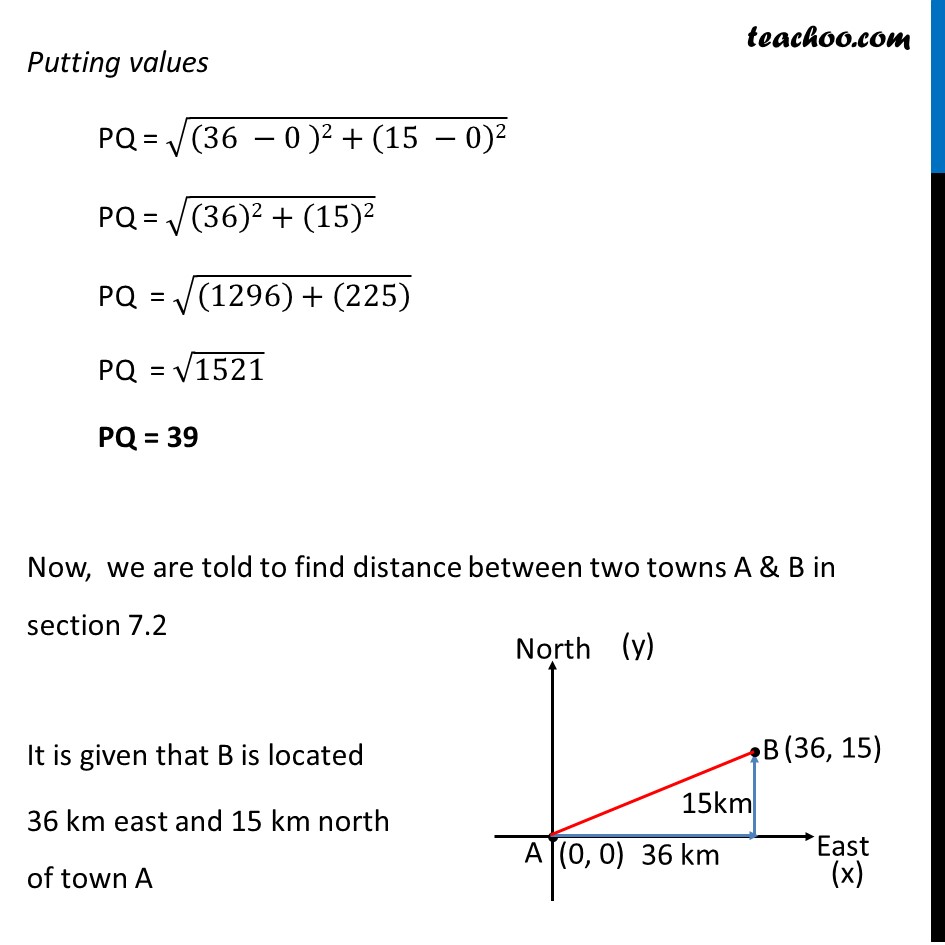
Ex 7.1 , 2 Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2. Let the two points be P(0, 0) & Q(36, 15) We need to find distance PQ PQ = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) Here, x1 = x coordinate of P = 0 y1 = y coordinate of P = 0 x2 = x coordinate of Q = 36 y2 = y coordinate of Q = 15 Putting values PQ = √((36 −0 )2+(15 −0)2) PQ = √((36)2+(15)2) PQ = √((1296)+(225) ) PQ = √1521 PQ = 39 Now, we are told to find distance between two towns A & B in section 7.2 It is given that B is located 36 km east and 15 km northof town ALet us take A as origin. Therefore, A will be A(0, 0) & B will be B(36, 15) We have to find distance AB AB = √((𝑥2 −𝑥1)2+(𝑦2 −𝑦1)2) Here, x1 = x coordinate of A = 0 y1 = y coordinate of A = 0 x2 = x coordinate of B = 36 y2 = y coordinate of B = 15 Putting values AB = √((36 −0 )2+(15 −0)2) = √((36)2+(15)2) = √((1296)+(225) ) = √1521 AB = 39 Therefore, the distance between the two towns is 39 km