Ex 6.2, 6 - Chapter 6 Class 10 Triangles (Important Question)

Transcript

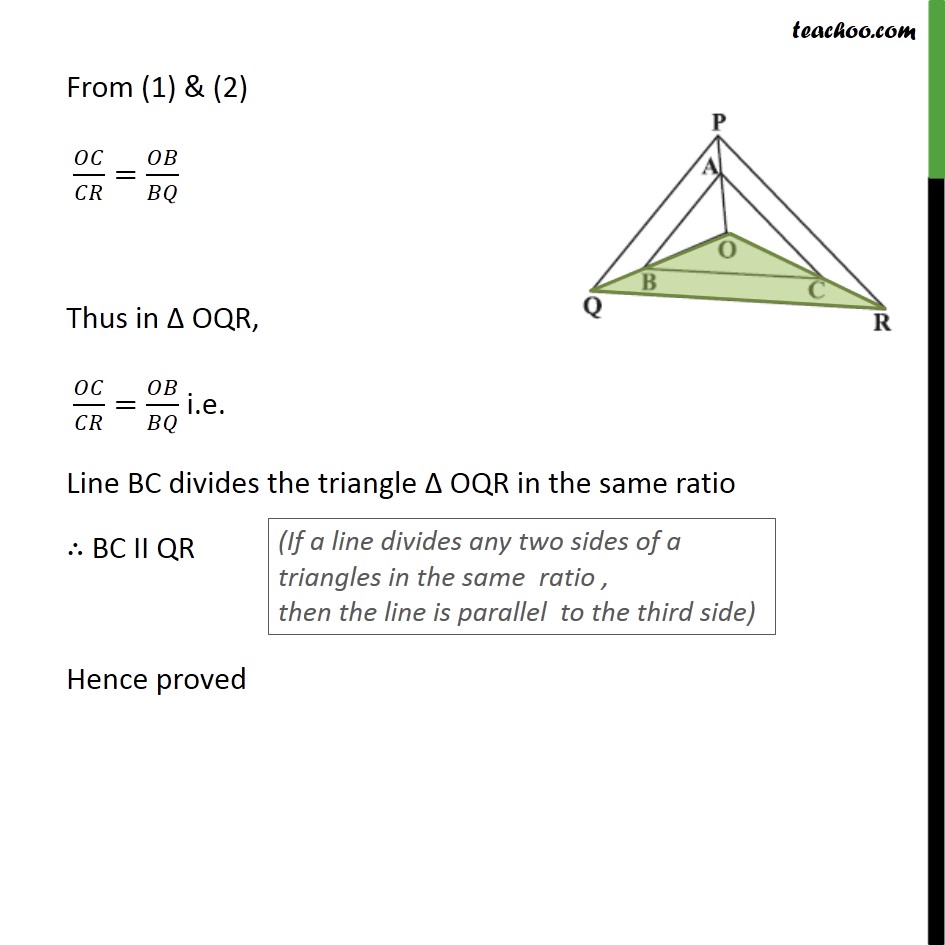
Ex 6.2, 6 In figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR. Given: AB II PQ and AC II PR To prove: BC II QR Proof: In ∆ 𝑂𝑃𝑄 AB II PQ (Line drawn parallel to one side of triangle, intersects the other two sides in distinct points, Then it divides the other 2 side in same ratio) 𝑂𝐴/𝐴𝑃=𝑂𝐵/𝐵𝑄 In ∆ 𝑂𝑃𝑅 AC II PR (Line drawn parallel to one side of triangle, intersects the other two sides in distinct points, Then it divides the other 2 side in same ratio) 𝑂𝐶/𝐶𝑅=𝑂𝐴/𝐴𝑃 From (1) & (2) 𝑂𝐶/𝐶𝑅=𝑂𝐵/𝐵𝑄 Thus in Δ OQR, 𝑂𝐶/𝐶𝑅=𝑂𝐵/𝐵𝑄 i.e. Line BC divides the triangle Δ OQR in the same ratio ∴ BC II QR (If a line divides any two sides of a triangles in the same ratio , then the line is parallel to the third side) Hence proved