Question 2 - NCERT Exemplar - MCQs - Chapter 12 Class 12 Linear Programming

Last updated at August 12, 2026 by

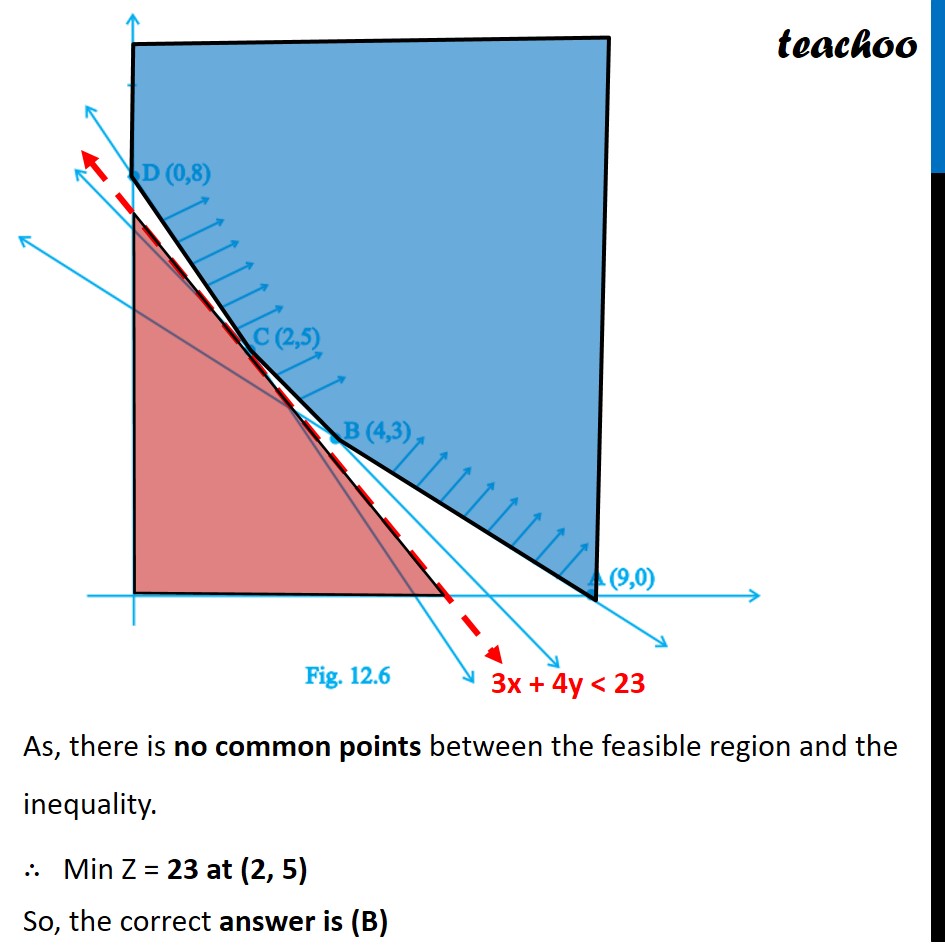
Feasible region (shaded) for a LPP is shown in the Fig. 12.6. Minimum of Z = 4x + 3y occurs at the point

(A) (0, 8)                           (B) (2, 5)

(C) (4, 3)                           (D) (9, 0)

This question is similar to Ex 12.2, 1 - Chapter 12 Class 12 - Linear Programming

Linear Programming [MCQ] - Feasible region (shaded) for a LPP is shown - NCERT Exemplar - MCQs

part 2 - Question 2 - NCERT Exemplar - MCQs - Serial order wise - Chapter 12 Class 12 Linear Programming
part 3 - Question 2 - NCERT Exemplar - MCQs - Serial order wise - Chapter 12 Class 12 Linear Programming

Take a fresh quiz. Then take another.
Every attempt is a new AI-adaptive Teachoo quiz with 3 questions, selected from your answers, mistakes, and progress.
Remove Ads
Teachoo · Class 12 Explore Class 12

Transcript

Question 2 Feasible region (shaded) for a LPP is shown in the Fig. 12.6. Minimum of Z = 4x + 3y occurs at the point (A) (0, 8) (B) (2, 5) (C) (4, 3) (D) (9, 0) Corners points are (0, 8), (2, 5), (4, 3) and (9, 0) We need to Minimise Z = 4x + 3y Checking value of Z at all corner points Since the feasible region is unbounded, Hence, 23 may or may not be the minimum value of Z So, we need to graph inequality : Z < 23 4x + 3y < 23 As, there is no common points between the feasible region and the inequality. ∴ Min Z = 23 at (2, 5) So, the correct answer is (B)

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh is an IIT Kanpur graduate and has been teaching for 16+ years. At Teachoo, he breaks down Maths, Science and Computer Science into simple steps so students understand concepts deeply and score with confidence.

Many students prefer Teachoo Black for a smooth, ad-free learning experience.