



Ex 3.1
Last updated at Dec. 13, 2024 by Teachoo





Transcript
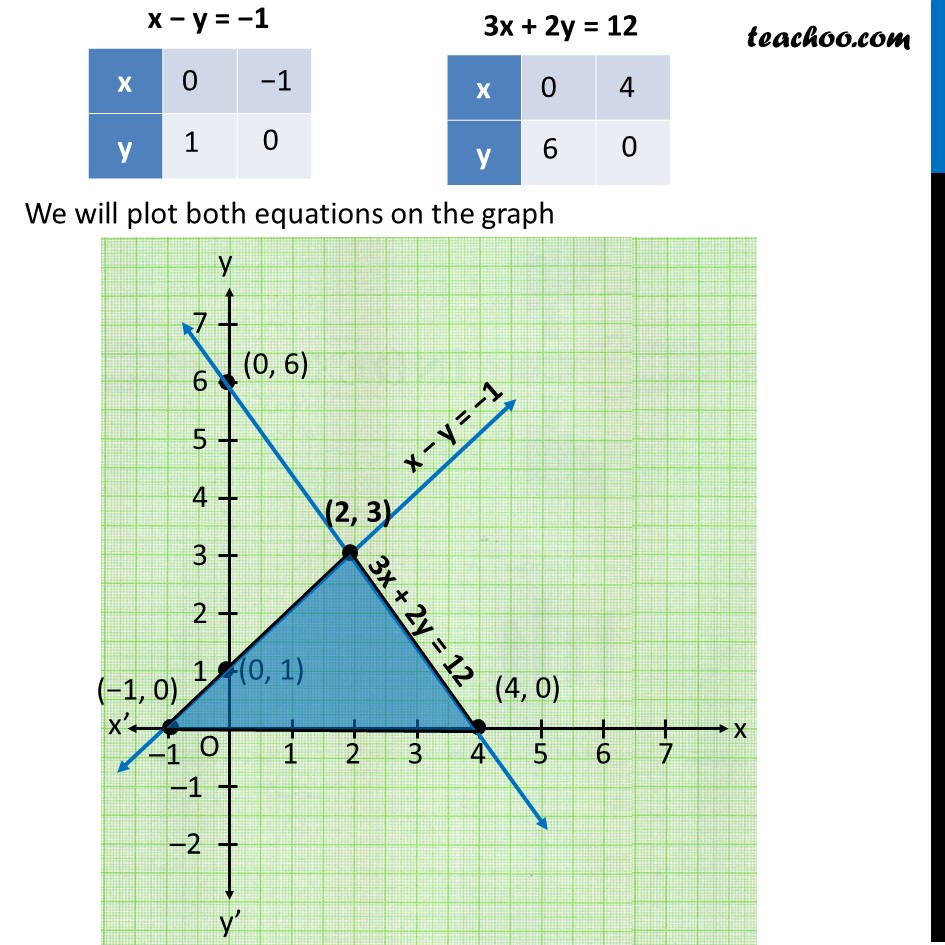
Ex 3.1, 7 Draw the graphs of the equations x – y + 1 = 0 and 3x+ 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region. Our equations are x – y = −1 3x + 2y = 12 Putting x = 0 0 − y = −1 −y = −1 y = 1 So, x = 0, y = 1 is a solution i.e. (0, 1) is a solution Putting y = 0 x − 0 = −1 x = −1 So, x = −1, y = 0 is a solution i.e. (−1, 0) is a solution Putting x = 0 3(0) + 2y = 12 2y = 12 y = 12/2 y = 6 So, x = 0, y = 6 is a solution i.e. (0, 6) is a solution Putting y = 0 3x + 2(0) = 12 3x = 12 x = 12/3 x = 4 So, x = 4, y = 0 is a solution i.e. (4, 0) is a solution We will plot both equations on the graph Therefore, the Required triangle is the triangle with vertices (2, 3), (–1, 0) & (4, 0)