Ex 3.1
Ex 3.1, 1 (ii) You are here
Ex 3.1, 2 (i)
Ex 3.1, 2 (ii)
Ex 3.1, 2 (iii)
Ex 3.1, 3 (i) Important
Ex 3.1, 3 (ii) Important
Ex 3.1, 3 (iii)
Ex 3.1, 3 (iv) Important
Ex 3.1, 3 (v)
Ex 3.1, 4 (i)
Ex 3.1, 4 (ii)
Ex 3.1, 4 (iii) Important
Ex 3.1, 4 (iv)
Ex 3.1, 5
Ex 3.1, 6 Important
Ex 3.1, 7 Important
Last updated at May 26, 2023 by Teachoo
Since NCERT Books are changed, we are still changing the name of content in images and videos. It would take some time.
But, we assure you that the question is what you are searching for, and the content is the best -Teachoo Promise. If you have any feedback, please contact us.
Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class
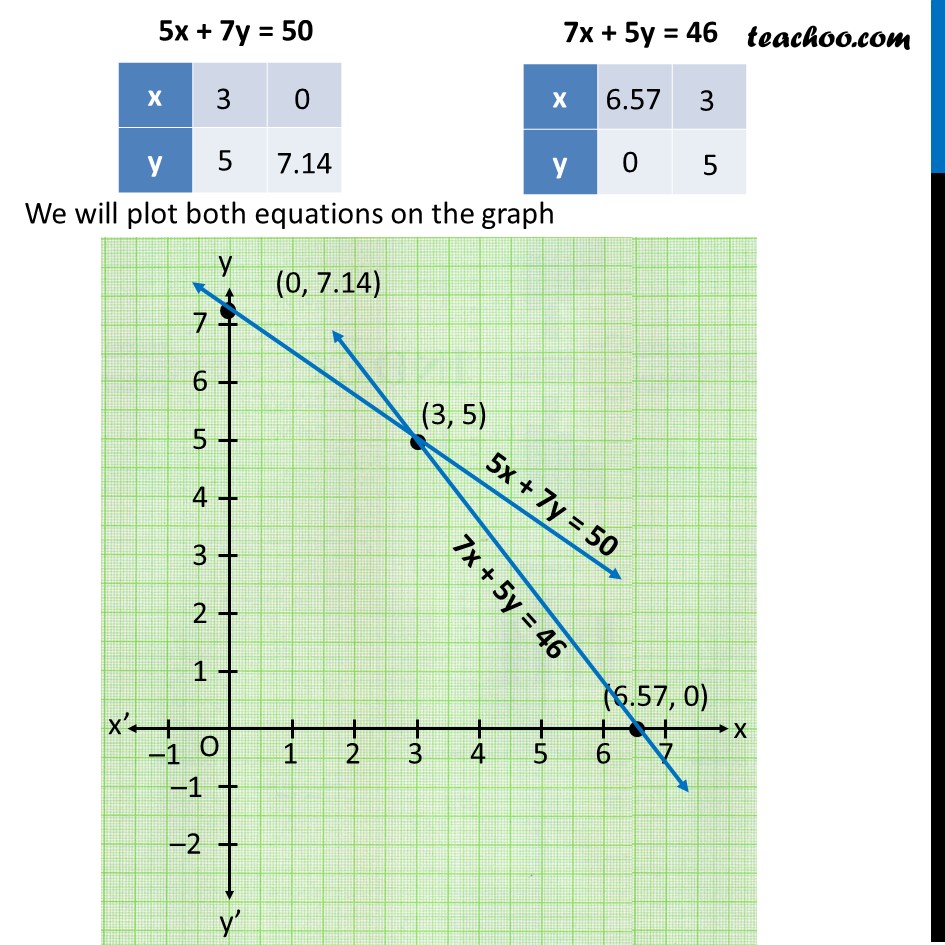
Ex 3.1, 1 Form the pair of linear equations in the following problems & find their solutions graphically (ii) 5 pencils and 7 pens together cost Rs. 50 , whereas 7 pencils and 5 pens together cost Rs. 46. Find the cost of one pencil and that of one pen Let the Cost of one Pencil be Rs x & Cost of one Pen be Rs y Given that 5 pencils and 7 pens together cost Rs 50 5 × (Cost of pencil) + 7 × (Cost of pens) = 50 5x + 7y = 50 Also, 7 pencils and 5 pens together cost Rs. 46 7 × (Cost of pencil) + 5 × (Cost of pen) = 46 7x + 5y = 46 Now, plotting equations 5x + 7y = 50 ...(1) 7x + 5y = 46 …(2) For Equation (1) 5x + 7y = 50 Let y = 5 5x + 7(5) = 50 5x + 35 = 50 5x + 35 = 50 − 35 5x = 15 x = 15/5 x = 3 So, x = 3, y = 5 is a solution i.e. (3, 5) is a solution Let x = 0 5(0) + 7y = 50 7y = 50 y = 50/7 y = 7.14 So, x = 0, y = 7.14 is a solution i.e. (0, 7.14) is a solution For Equation (2) 7x + 5y = 46 Let y = 0 7x + 5(0) = 46 7x = 46 x = 46/7 x = 6.57 So, x = 6.57, y = 0 is a solution i.e. (6.57, 0) is a solution Let x = 3 7(3) + 5y = 46 21 + 5y = 46 5y = 46 − 21 5y = 25 y = 25/5 y = 5 So, x = 3, y = 5 is a solution i.e. (3, 5) is a solution We will plot both equations on the graph Therefore, Solution of the equations is (3, 5) Thus, Cost of 1 Pencil = x = Rs 3 Cost of 1 Pen = y = Rs 5
