Question 18 - NCERT Exemplar - MCQ - Chapter 7 Class 10 Coordinate Geometry (Term 1)

Transcript

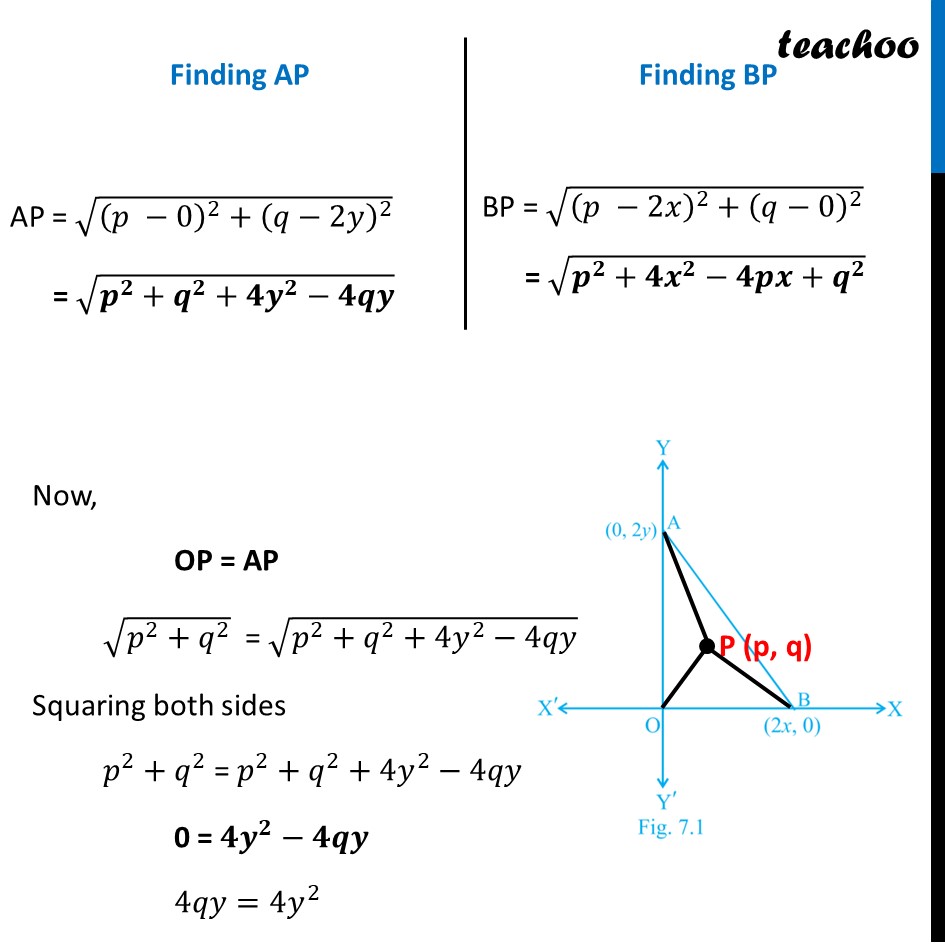
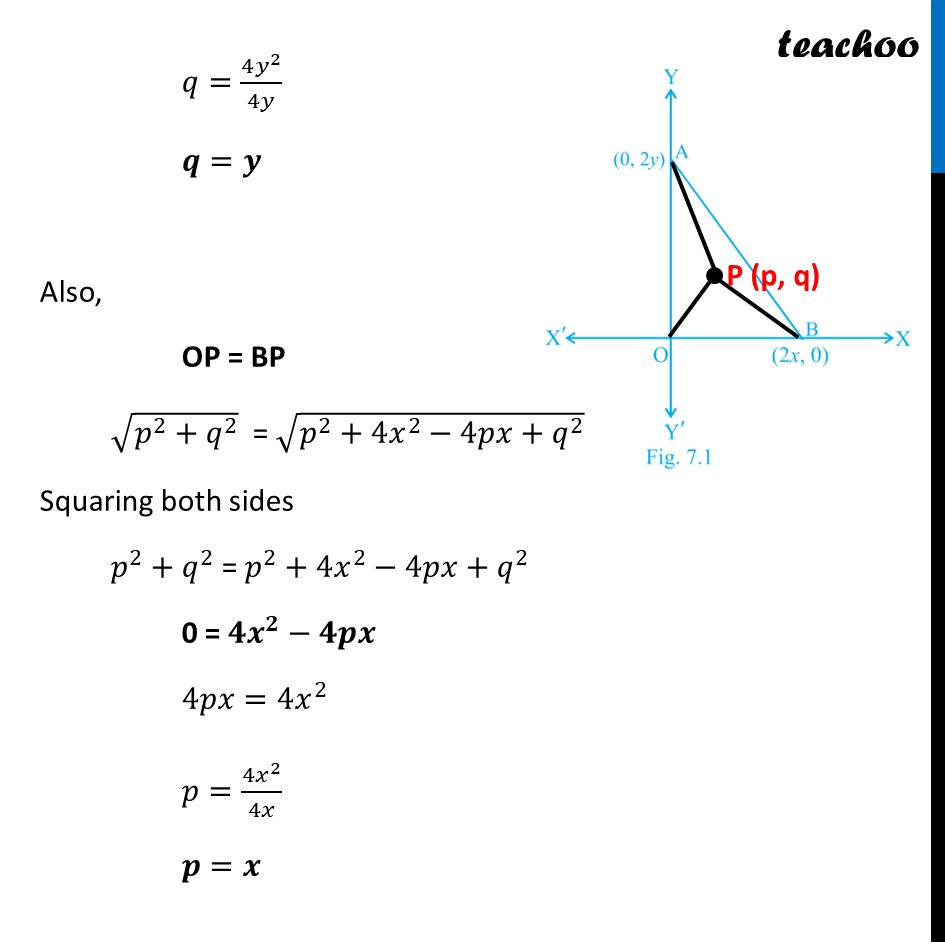
Question 18 The coordinates of the point which is equidistant from the three vertices of the ∆ AOB as shown in the Fig. 7.1 is (x, y) (B) (y, x) (C) (𝑥/2,𝑦/2) (D) (𝑥/2,𝑦/2) Let Required point = P (p, q) Since point P is equidistant from A, B & C Hence, OP = AP = BP Now, OP =√(( 𝑝 −0)^2+(𝑞−0)^2 ) = √(𝒑^𝟐+𝒒^𝟐 ) Finding AP AP = √((𝑝 −0)^2+(𝑞−2𝑦)^2 ) = √(𝒑^𝟐+𝒒^𝟐+𝟒𝒚^𝟐−𝟒𝒒𝒚) Finding BP BP = √((𝑝 −2𝑥)^2+(𝑞−0)^2 ) = √(𝒑^𝟐+𝟒𝒙^𝟐−𝟒𝒑𝒙+𝒒^𝟐 ) Now, OP = AP √(𝑝^2+𝑞^2 ) = √(𝑝^2+𝑞^2+4𝑦^2−4𝑞𝑦) Squaring both sides 𝑝^2+𝑞^2 = 𝑝^2+𝑞^2+4𝑦^2−4𝑞𝑦 0 = 𝟒𝒚^𝟐−𝟒𝒒𝒚 4𝑞𝑦=4𝑦^2 𝑞=(4𝑦^2)/4𝑦 𝒒=𝒚 Also, OP = BP √(𝑝^2+𝑞^2 ) = √(𝑝^2+4𝑥^2−4𝑝𝑥+𝑞^2 ) Squaring both sides 𝑝^2+𝑞^2 = 𝑝^2+4𝑥^2−4𝑝𝑥+𝑞^2 0 = 𝟒𝒙^𝟐−𝟒𝒑𝒙 4𝑝𝑥=4𝑥^2 𝑝=(4𝑥^2)/4𝑥 𝒑=𝒙 Thus, Coordinates of Point P = (p, q) = (x, y) So, the correct answer is (D)