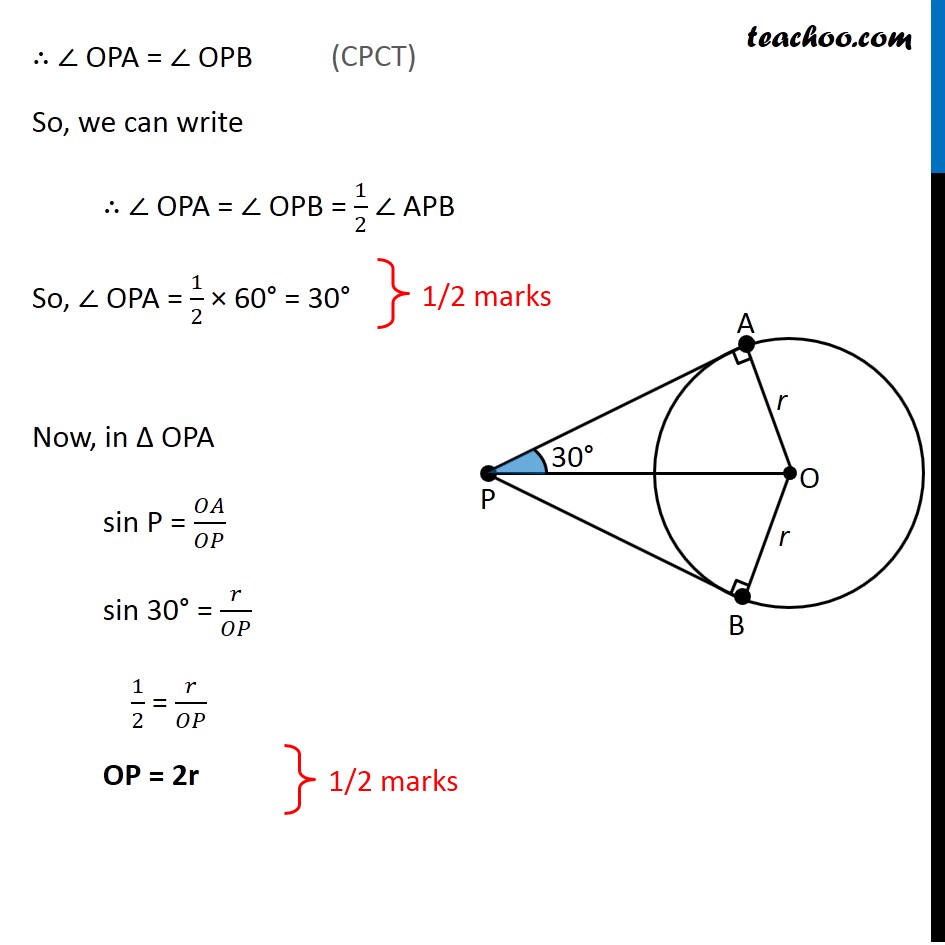
If the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and centre O is 60° , then find the length of OP.

CBSE Class 10 Sample Paper for 2020 Boards - Maths Standard
CBSE Class 10 Sample Paper for 2020 Boards - Maths Standard
Last updated at Dec. 16, 2024 by Teachoo


Transcript
Question 18 (OR 1st question) If the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and center O is 60° , then find the length of OP. Given that Angle between two tangents is 60° ∴ ∠ APB = 60° Now, In Δ OPA and Δ OPB ∠ OAP = ∠ OBP OP = OP OA = OB ∴ Δ OPA ≅ Δ OPB ∴ ∠ OPA = ∠ OPB So, we can write ∴ ∠ OPA = ∠ OPB = 1/2 ∠ APB So, ∠ OPA = 1/2 × 60° = 30° Now, in Δ OPA sin P = 𝑂𝐴/𝑂𝑃 sin 30° = 𝑟/𝑂𝑃 1/2 = 𝑟/𝑂𝑃 OP = 2r