Question 10 - Important Questions on Circles - Chapter 9 Class 9 Circles

Transcript

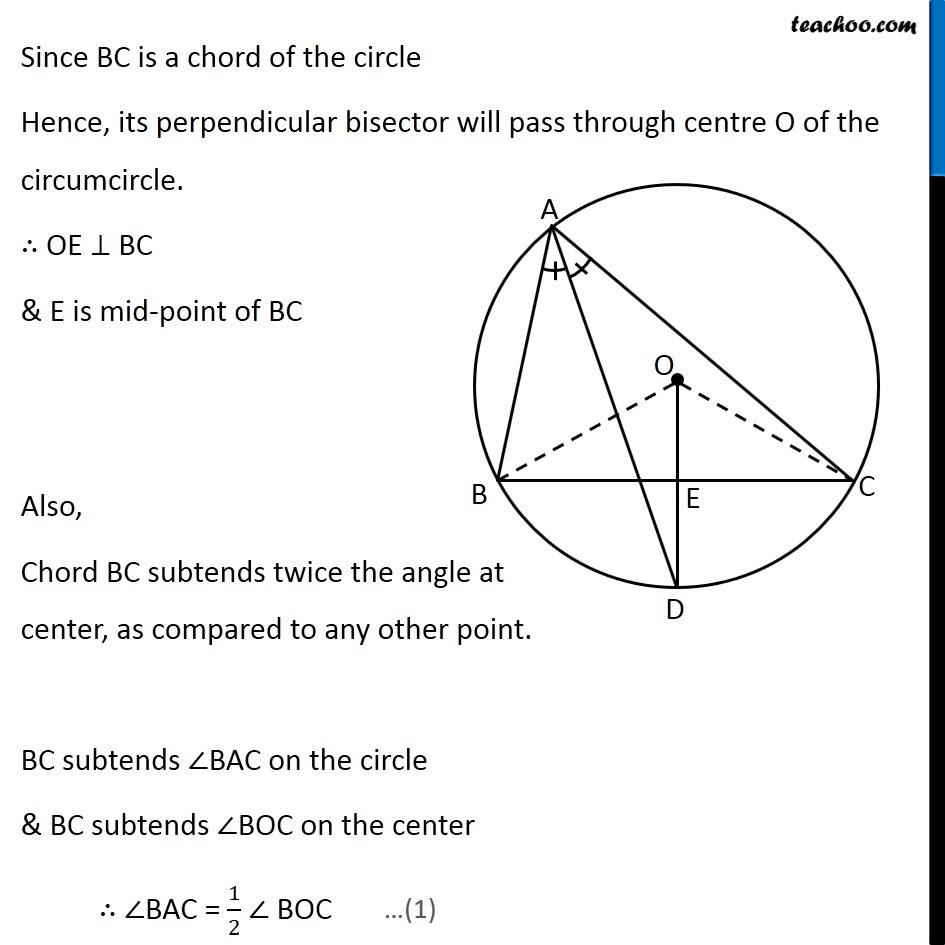
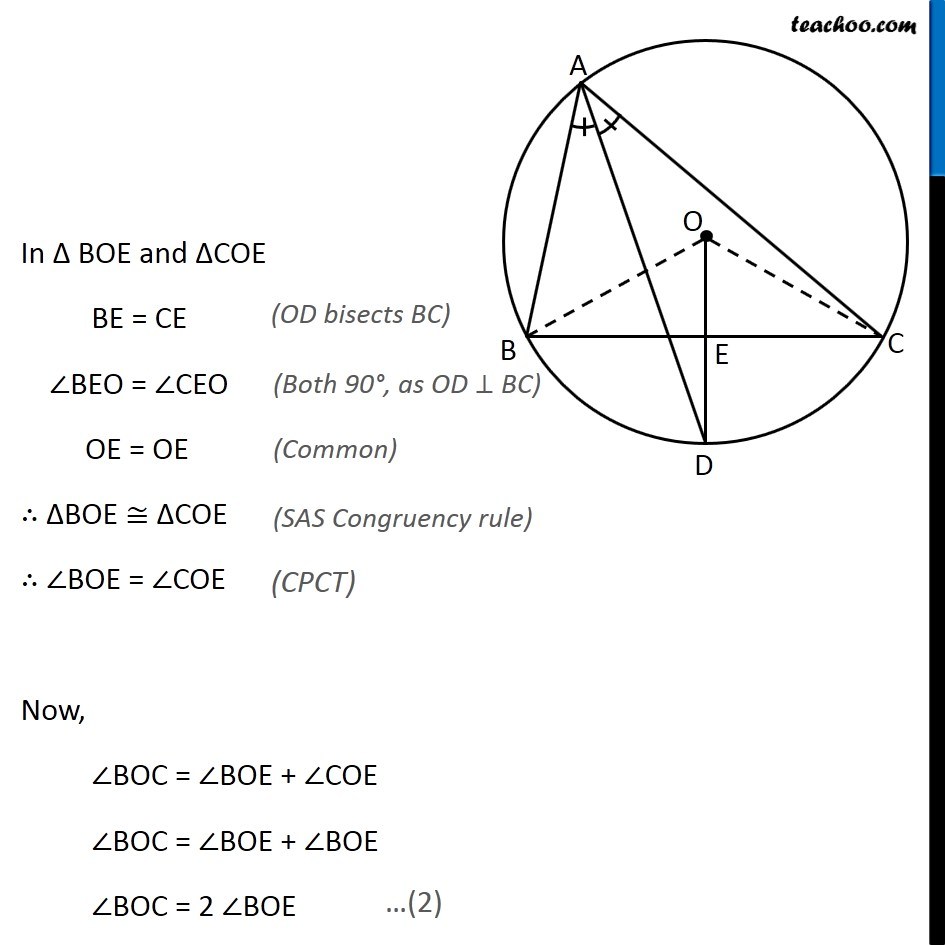
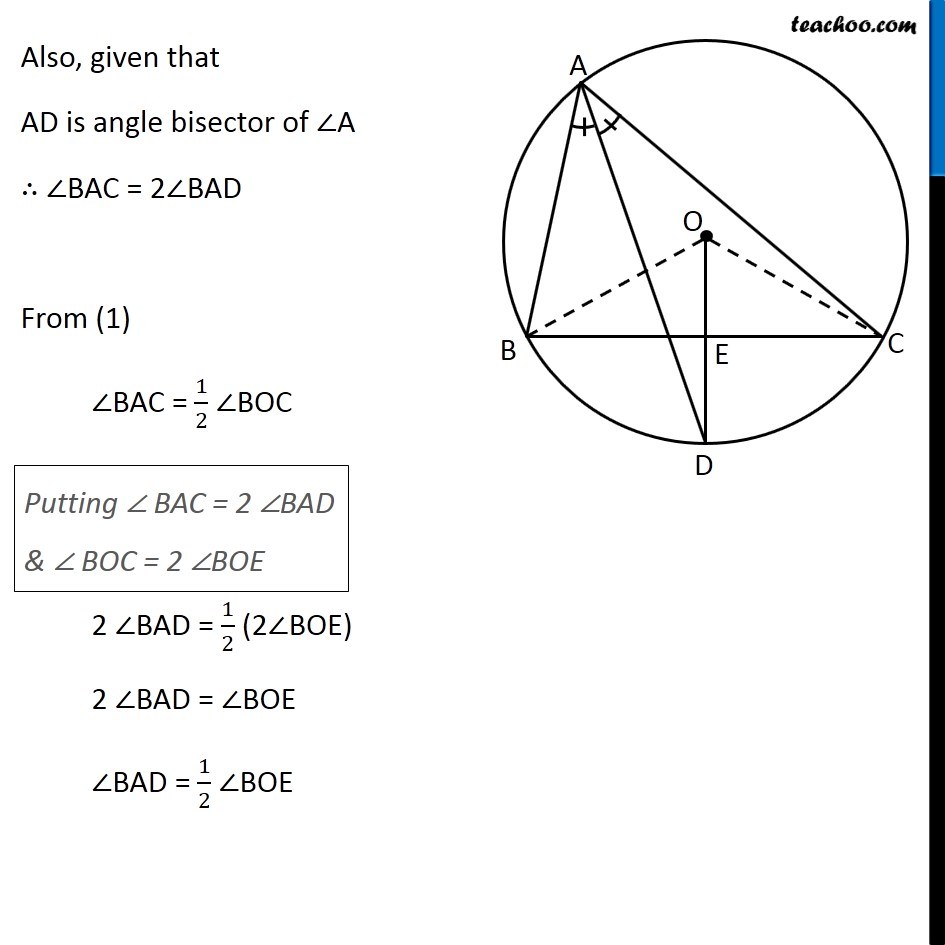
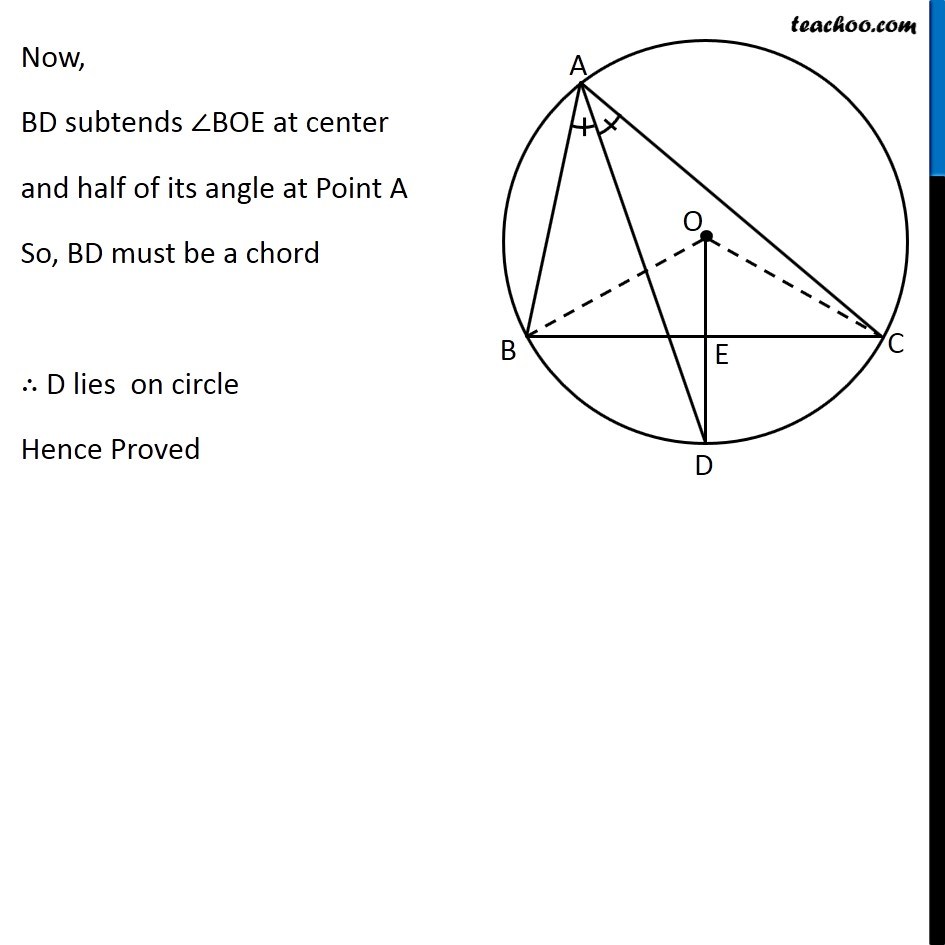
Question 10 In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC Circumcircle is a circle where all 3 vertices of triangle are on the circle Given: In ∆ABC, AD is angle bisector of ∠A and OD is perpendicular bisector of BC, intersecting each other at point D. To Prove: D lies on the circle Construction: Join OB and OC Proof: Since BC is a chord of the circle Hence, its perpendicular bisector will pass through centre O of the circumcircle. ∴ OE ⊥ BC & E is mid-point of BC Also, Chord BC subtends twice the angle at center, as compared to any other point. BC subtends ∠BAC on the circle & BC subtends ∠BOC on the center ∴ ∠BAC = 1/2 ∠ BOC In ∆ BOE and ∆COE BE = CE ∠BEO = ∠CEO OE = OE ∴ ∆BOE ≅ ∆COE ∴ ∠BOE = ∠COE Now, ∠BOC = ∠BOE + ∠COE ∠BOC = ∠BOE + ∠BOE ∠BOC = 2 ∠BOE (OD bisects BC) (Both 90°, as OD ⊥ BC) (Common) (SAS Congruency rule) (CPCT) …(2) Also, given that AD is angle bisector of ∠A ∴ ∠BAC = 2∠BAD From (1) ∠BAC = 1/2 ∠BOC Putting ∠ BAC = 2 ∠BAD & ∠ BOC = 2 ∠BOE 2 ∠BAD = 1/2 (2∠BOE) 2 ∠BAD = ∠BOE ∠BAD = 1/2 ∠BOE Now, BD subtends ∠BOE at center and half of its angle at Point A So, BD must be a chord ∴ D lies on circle Hence Proved