Question 9 - Important Questions on Circles - Chapter 9 Class 9 Circles

Transcript

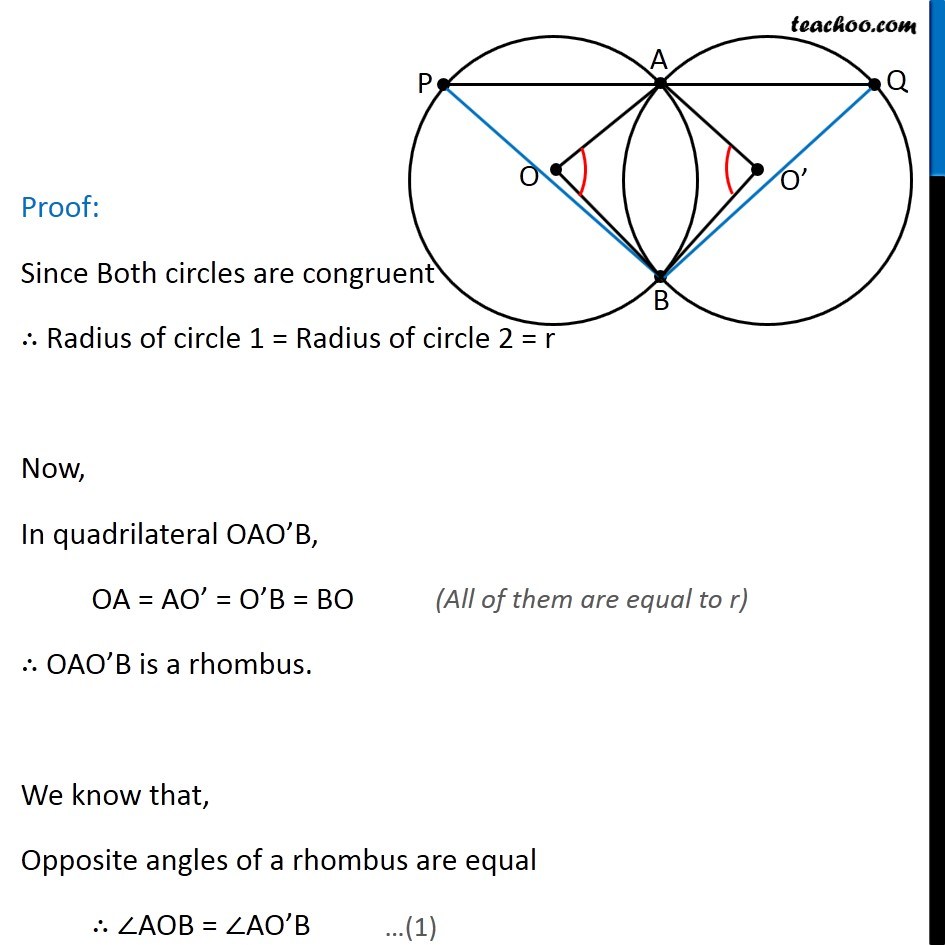
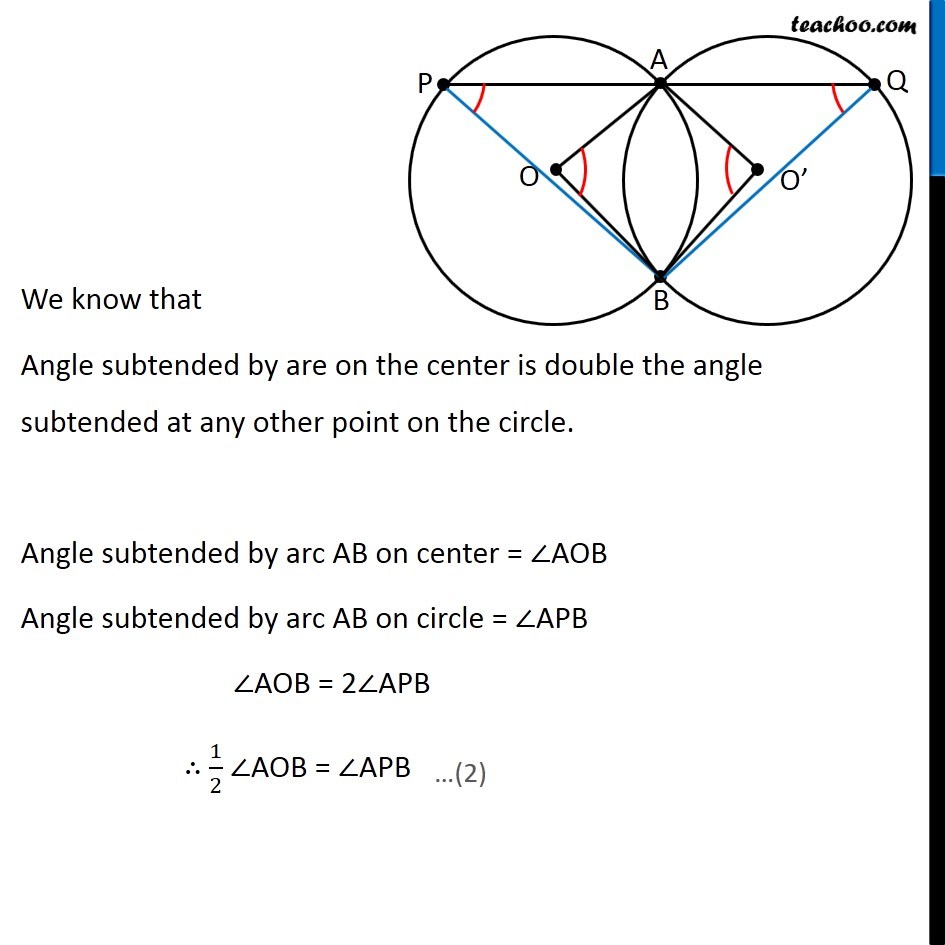
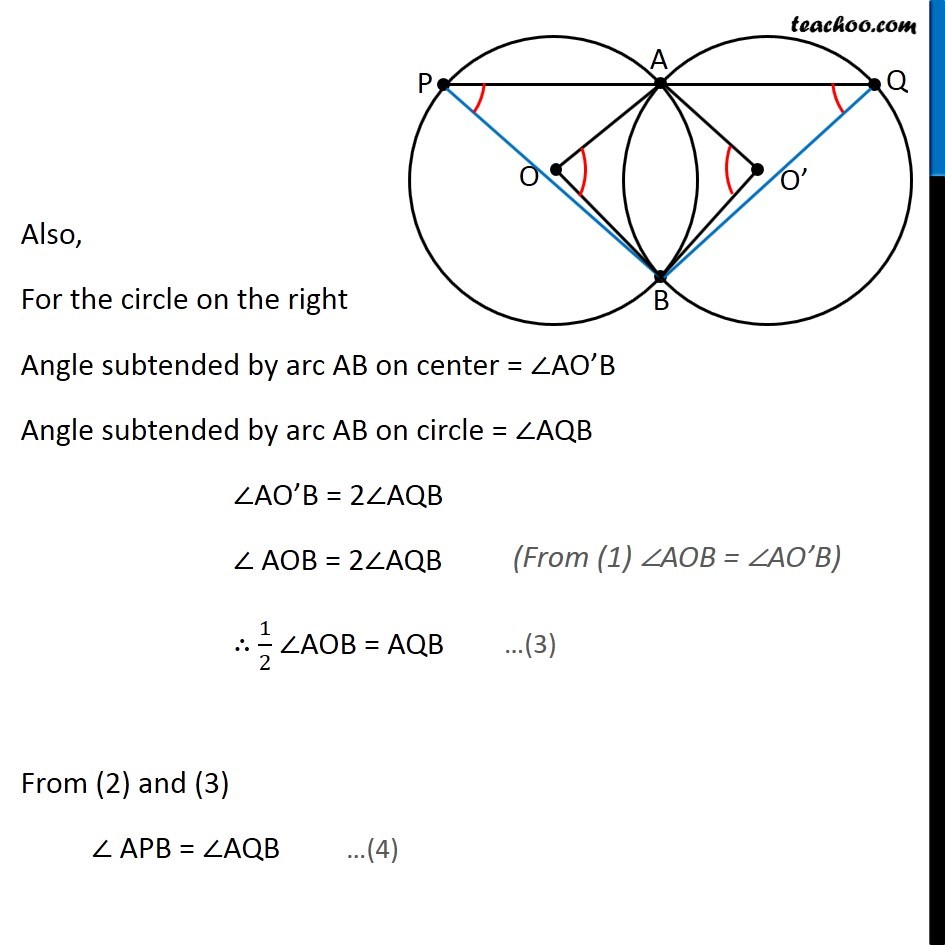
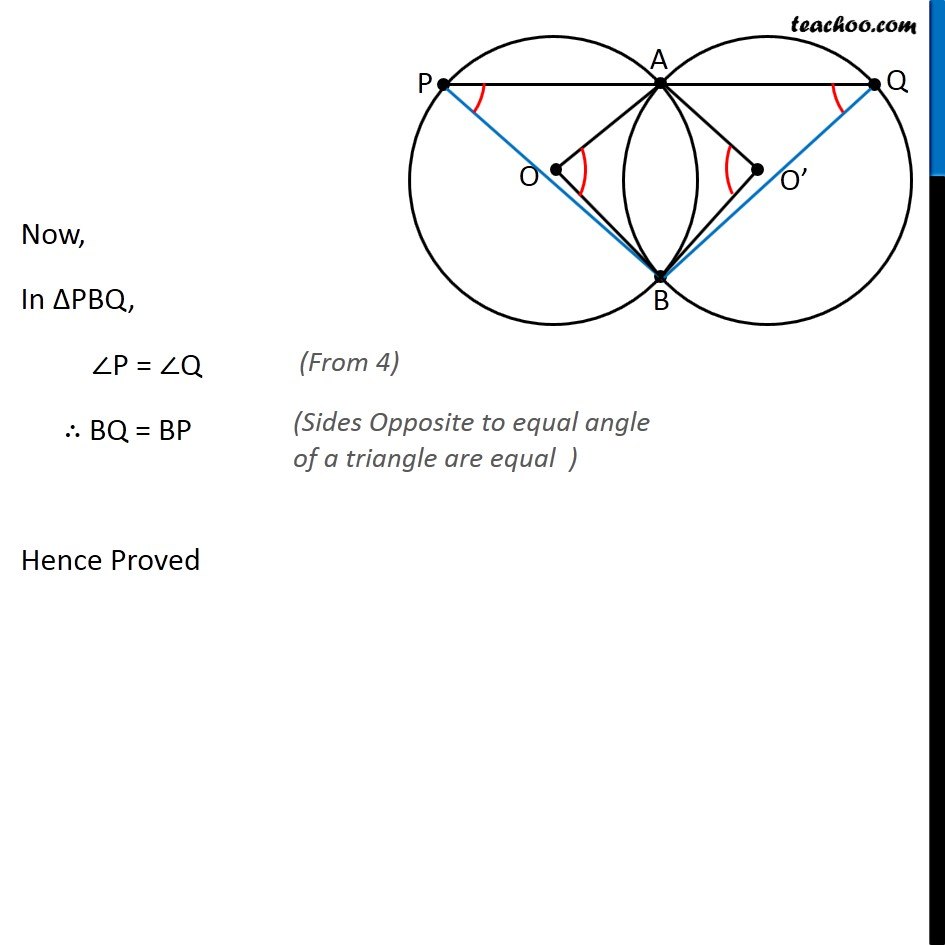
Question 9 Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ Given: Two congruent circles intersecting each other at points A & B, P and Q lie on the two circles To Prove: BP = BQ Construction: Join OA, OB, O’A, O’B Proof: Since Both circles are congruent ∴ Radius of circle 1 = Radius of circle 2 = r Now, In quadrilateral OAO’B, OA = AO’ = O’B = BO ∴ OAO’B is a rhombus. We know that, Opposite angles of a rhombus are equal ∴ ∠AOB = ∠AO’B (All of them are equal to r) We know that Angle subtended by are on the center is double the angle subtended at any other point on the circle. Angle subtended by arc AB on center = ∠AOB Angle subtended by arc AB on circle = ∠APB ∠AOB = 2∠APB ∴ 1/2 ∠AOB = ∠APB Also, For the circle on the right Angle subtended by arc AB on center = ∠AO’B Angle subtended by arc AB on circle = ∠AQB ∠AO’B = 2∠AQB ∠ AOB = 2∠AQB ∴ 1/2 ∠AOB = AQB From (2) and (3) ∠ APB = ∠AQB (From (1) ∠AOB = ∠AO’B) Now, In ∆PBQ, ∠P = ∠Q ∴ BQ = BP Hence Proved (From 4) (Sides Opposite to equal angle of a triangle are equal )